10. Общие условия устойчивости линейных систем.
Пусть лин.САР опис.сист.дифф.ур-ий dxi/dt=ai1x1+ ai2x2+…ainxn+Fi(t),где i=1…n Реш.этого ур-я сост.из реш.ур-я свободного движ. и вынужд. xi(t)= xiсв(t)- xiвозм(t),тогда ур-ие свободного движ.выразится в xid(t)= xi(t)- xiвозм(t). В соотв. с опр-ем устойчивости по Ляпунову можно утверждать что лин.сист.будет устойчивой if отклонение возмущ.движ.от невозмущ.стремится к 0 с течением времени.Необхюи достаточным условием асимптотич.устойчивости явл вып.требования об отриц.частях всех корней характерестич-о ур-я. Пусть реш.ур-я свободн.движ.имеет вид xiсв(t)=∑Cieλiῑ где с,в некие константы задан.в нач. и Сi. В общем случаем корни характ-ого ур-я явл комплексными anλn+…a1λ+a0 λi=αi+-jwi корень λi м.б.предст.на комплексной пл-ти. Люб.полупл.соотв.отриц.частотам. Остюда можно сформ.геометрич.опр-ие устойчивости:необх.и.достат.усл.устойчив.сист.явл располож.корней характер.ур-я в левой пл-ти,границы устойчивости явл 1) λi=0 наличие нулевого корня,апериодич.граница 2)наличие пары чисто мнимых корней λ1,2=+-jw – колебат.граница 3)наличие ͚корня λi= ͚
11. Критерий устойчивости Гурвица.
Устойчивость САР является одним из важнейших условий работоспособности этой системы.
Если под влиянием возмущения система отклоняется от состояния равновесия или заданного закона движения, а после прекращения действия внешнего возмущения снова возвращается к исходному состоянию, то движение в системе является устойчивым, сходящимся к исходному состоянию. Т. о. под устойчивостью линейной системы понимают свойство затухания переходного процесса с течением времени.
Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.
Система устойчива «в малом», если определен факт наличия устойчивости, но не определены его границы.
Система устойчива «в большом», когда определен факт наличия устойчивости, выявлены границы устойчивости и то, что реальные отклонения не выходят за эти границы.
В
большинстве случаев вычисление корней
уравнения для определения устойчивости
крайне затруднительно, поэтому были
введены критерии, позволяющие судить
об устойчивости системы по коэффициентам
характеристического уравнения без
вычисления его корней. Пусть
характеристическое уравнение системы
имеет следующий вид:
.
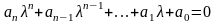Необходимо и достаточно, чтобы при a0
>0
были положительными n
главных определителей матрицы Гурвица:
,
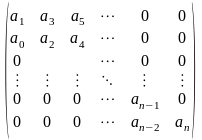где n
– порядок характеристического уравнения.
Правило построения матрицы: по главной диагонали располагаются коэффициенты с a1 по an. Строки состоят поочередно из коэффициентов либо только с четными, либо только с нечетными индексами. Каждая такая пара строк сдвинута относительно предыдущей пары на позицию вправо. То есть, от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз, а на место коэффициентов с индексами меньше нуля ставятся нули.
Т. о. при n ≤ 2 положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости САУ. При n >2 появляются дополнительные условия для определителей.
Критерий Гурвица применяют при n ≤ 4. При больших порядках возрастает число определителей и и процесс становится трудоемким.
Недостаток: малая наглядность, резкое увеличение количества расчетов с увеличением порядка системы.
Достоинство: удобен для реализации на ЭВМ. Часто используется для определения влияния одного из параметров САУ на ее устойчивость