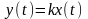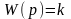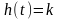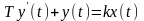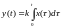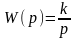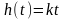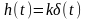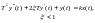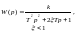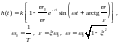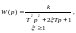8. Передаточные функции и частотные характеристики типовых звеньев системы автоматического регулирования.

Тип звена	Дифференциальное уравнение	Передаточная функция	Переходная характеристика
Безынерци- оное
Инерционное первого порядка
Интегрирующее идеальное
Дифференциру- ющее идеальное
Дифференциру- ющее реальное
Колебательное
Апериодичес- кое второго порядка

9. Понятие устойчивости системы по Ляпунову.

Устойчивость САР является одним из важнейших условий работоспособности этой системы.

Если под влиянием возмущения система отклоняется от состояния равновесия или заданного закона движения, а после прекращения действия внешнего возмущения снова возвращается к исходному состоянию, то движение в системе является устойчивым, сходящимся к исходному состоянию. Т. о. под устойчивостью линейной системы понимают свойство затухания переходного процесса с течением времени.

Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.

Система устойчива «в малом», если определен факт наличия устойчивости, но не определены его границы.

Система устойчива «в большом», когда определен факт наличия устойчивости, выявлены границы устойчивости и то, что реальные отклонения не выходят за эти границы.

Полагаем, что диф. уравнение динамики системы записано в следующем виде: 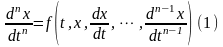. Это уравнение может быть представлено в виде системы из n уравнений первого порядка: 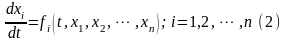. Будем считать, что уравнение (2) описывает не возмущающее движение системы, а обобщенные координаты x_i в начальный момент времени t = t0 имеют значения:

/*Решение системы (2) определяется начальными условиями (3) и может быть записано в виде: . Так как решение этого уравнения должно удовлетворять начальному условию t = t0, то его подстановка дает нам , что показывает состояние системы в начальный момент времени. */

Движение системы при измененных начальных условиях называется возмущенным движением. Пусть 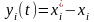, тогда уравнение (2) преобразуется в - эта система называется системой уравнений возмущенного движения, а переменная y_i – отклонением координат x_i .

Т. о., движение называется устойчивым по Ляпунову, если при небольших изменениях начальных значений x_i (при малых начальных возмущениях) возмущенное движение в момент времени t > t0 будет отличаться от невозмущенного сколь угодно мало.

Движение называется асимптотически устойчивым, если устойчивое возмущенное и невозмущенное движения, являясь близкими по значению в начальный момент времени t = t0, не только остаются близкими во все последующие моменты, но и неограниченно сближаются с течением времени. Если движение является асимптотически устойчивым при любых больших начальных отклонениях, то система называется асимптотически устойчивой в целом. – уравнения первого приближения.

Существует три теоремы Ляпунова об устойчивости по первому приближению.

Теорема 1: если все корни уравнения (6) имеют отрицательные вещественные части, то движение асимптотически устойчиво при малых начальных отклонениях независимо от вида малых нелинейностей y_i.

Теорема 2: если среди корней уравнения (6) есть хотя бы один корень с положительной вещественной частью, то движение неустойчиво независимо от малых нелинейностей y_i.

Теорема 3: в случае наличия среди корней уравнения (6) корня с нулевой вещественной частью при всех остальных отрицательных ничего нельзя сказать об устойчивости движения без специального исследования уравнения с малыми нелинейностями y_i.