
- •1. Классические принципы управления.
- •2. Основные определения теории автоматического регулирования.
- •3. Классификация систем автоматического регулирования.
- •1) По характеру изменения управляющего воздействия:
- •5. Составление и линеаризация дифференциальных уравнений в теории автоматического регулирования.
- •6. Понятие передаточной функции и частотных характеристик системы автоматического регулирования.
- •7. Классификация типовых звеньев системы автоматического регулирования.
- •8. Передаточные функции и частотные характеристики типовых звеньев системы автоматического регулирования.
- •9. Понятие устойчивости системы по Ляпунову.
- •10. Общие условия устойчивости линейных систем.
- •11. Критерий устойчивости Гурвица.
- •12. Критерий устойчивости Михайлова.
- •13. Критерий устойчивости Найквиста.
- •14. Понятие точности систем автоматического регулирования.
- •15. Качество переходного процесса.
- •16. Частотные методы оценки качества переходного процесса.
- •17. Корневые методы оценки качества переходного процесса.
- •18. Интегральные методы оценки качества переходного процесса.
- •19. Классификация корректирующих устройств для линейных систем: последовательные и параллельные корректирующие устройства.
- •21. Постановка задачи синтеза корректирующих устройств.
- •22. Основные понятия и типы дискретных систем.
- •23. Сущность и свойства импульсных систем.
- •24. Сущность и свойства цифровых систем.
- •25. Нелинейные системы автоматического регулирования. Классификация нелинейностей.
- •26. Понятие фазового пространства и фазовой плоскости.
- •27. Общие представления о процессе развития систем управления.
- •28.Общее информационное представление системы управления.
- •29. Информационные структуры систем управления.
- •30. Развитие систем управления в виде индивидуальной адаптации.
- •31. Классификация адаптивных систем.
- •32.Развитие систем управления в виде групповой адаптации.
- •33. Структуры и свойства систем группового поведения.
22. Основные понятия и типы дискретных систем.
В ходе процесса управления наряду с непрерывными (аналоговыми) системами широко используются дискретные системы (ДС), в которых контур управления замыкается только на определенный промежуток времени, осуществляя воздействие на исполнительный элемент импульсами. В паузах между импульсами цепь управления остается разомкнутой.
НЧ – непрерывная часть
УУ – устройство управления
КУ – корректирующее устройство
О – объект
ИЭ – исполнительный элемент
ЭС – элемент сравнения
ЗЭ – задающий элемент
КЦ – корректирующая цепь (на границе)
Имп. Э – импульсный элемент
Упрощенная схема:
ε(t) преобразуется импульсным элементом в последовательность α(t). Процесс преобразования непрерывной функции ε(t) в дискретную функцию α(t) называется квантованием (дискретизацией).
По способам квантования дискретные системы делятся на три вида:
1) По времени квантования (импульсные системы)
2) По уровню квантования (релейные системы)
3) По времени и по уровню квантования одновременно (цифровые системы)
23. Сущность и свойства импульсных систем.
В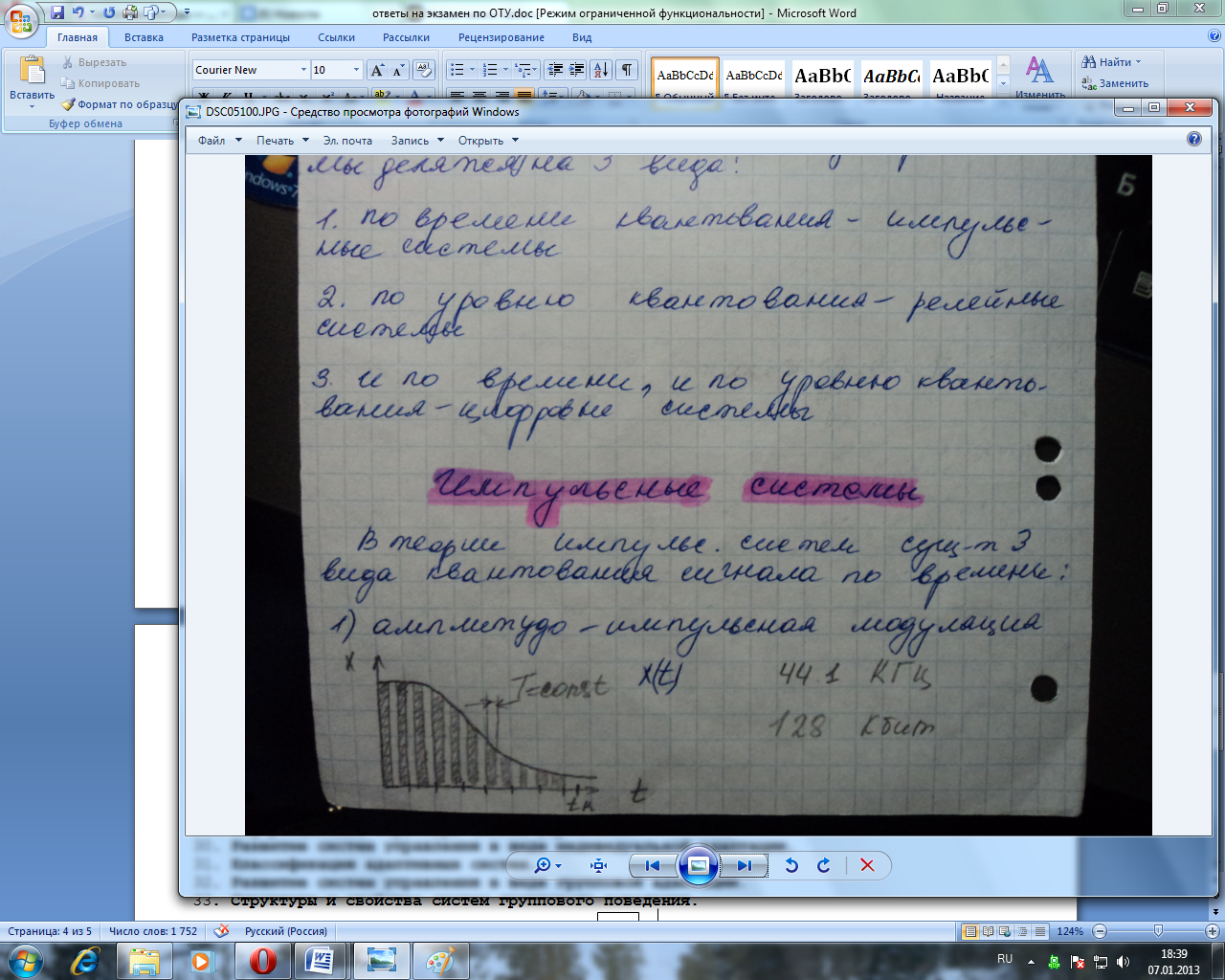
 теории импульсных систем сущ.3 вида
квантования сигнала по
времени:
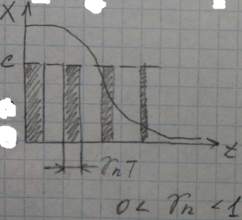
а) амплитудно-импульсные модуляци -
амплитуда импульса пропорциональна
вх.сигналу б) широтно-импульсная
модуляция – ширина импульса пропорциональна
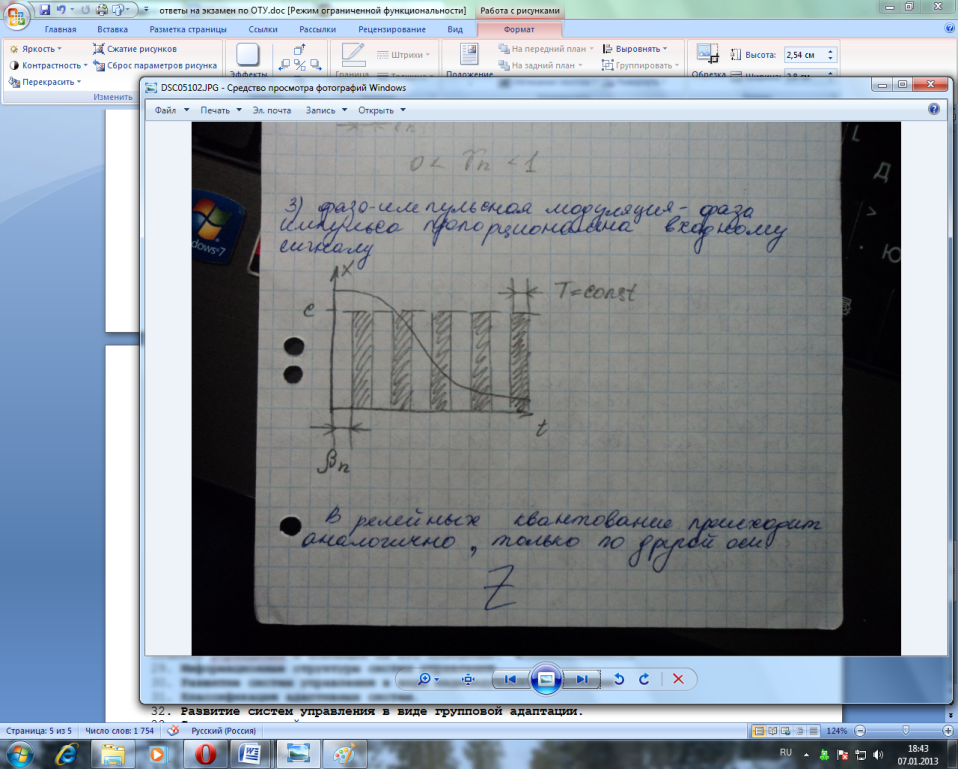
вх.сигналу в) фазо-импульсная модуляция
– фаза импулься пропорциональна
вх.сигналу.
теории импульсных систем сущ.3 вида
квантования сигнала по
времени:
а) амплитудно-импульсные модуляци -
амплитуда импульса пропорциональна
вх.сигналу б) широтно-импульсная
модуляция – ширина импульса пропорциональна
вх.сигналу в) фазо-импульсная модуляция
– фаза импулься пропорциональна
вх.сигналу.
24. Сущность и свойства цифровых систем.
Т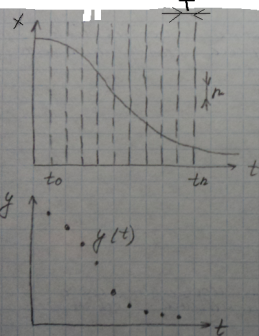
 акой
перевод непрерывной ф-ии x(t)
в цифровую y(t)
в опрд-ой сист. счисления наз-я
импульсно-кодовой
модуляцией.
Близость к решетчатой(цифровой)ф-ии
y(t)
к значениям x(t)
зависит от кол-ва разрядов цофр.устр-ва(h)
и от периода квантования T.
В цифр.устр-ах обычно величина x(t)
получается в рез-те вычисления по опр-му
алгоритму в непосредственно цифровом
виде y(t).
АВ-алгоритм вычисления ЭЗ-эл-т запаздывания
Эл-т ИКМ-эл-т импульсно-кодовой модуляции
Н/Д-преобраз-ть непрерывной величины
в дискретную ЦВУ-цифровое вычислит.устр-во
акой
перевод непрерывной ф-ии x(t)
в цифровую y(t)
в опрд-ой сист. счисления наз-я
импульсно-кодовой
модуляцией.
Близость к решетчатой(цифровой)ф-ии
y(t)
к значениям x(t)
зависит от кол-ва разрядов цофр.устр-ва(h)
и от периода квантования T.
В цифр.устр-ах обычно величина x(t)
получается в рез-те вычисления по опр-му
алгоритму в непосредственно цифровом
виде y(t).
АВ-алгоритм вычисления ЭЗ-эл-т запаздывания
Эл-т ИКМ-эл-т импульсно-кодовой модуляции
Н/Д-преобраз-ть непрерывной величины
в дискретную ЦВУ-цифровое вычислит.устр-во
25. Нелинейные системы автоматического регулирования. Классификация нелинейностей.
Нелинейной САР наз-я такая сист.кот.содержит хотябы одно звено,опис-ое нелинейным ур-ем. Классиф.нелинейностей: Статические непрерывные[парабола,синусоида] релейные(дискретные) однозначные петлевые комплексные Динамические нелинейности возникают в САР в силу естественных причин, таких как запаздываие,гистерезис.
26. Понятие фазового пространства и фазовой плоскости.
Фазовое пространство в математике и физике — пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства.
Сущность понятия фазового пространства заключается в том, что состояние сколь угодно сложной системы представляется в нём одной единственной точкой, а эволюция этой системы — перемещением этой точки. Кроме того, в механике движение этой точки определяется сравнительно простыми уравнениями Гамильтона, анализ которых позволяет делать заключения о поведении сложных механических систем.
Механические системы: В случае механических систем это пространство четной размерности, координатами в котором являются обычные пространственные координаты (или обобщённые координаты) частиц системы и их импульсы (или обобщённые импульсы).
Например, фазовое пространство для системы, состоящей из одной свободной материальной точки, имеет 6 измерений, три из которых — это три обычные координаты, а ещё три — это компоненты импульса. Соответственно, фазовое пространство для системы из двух свободных материальных точек будет содержать 12 измерений и т. д.
Динамические системы: В теории динамических систем и теории дифференциальных уравнений фазовое пространство является более общим понятием. Оно не обязательно чётномерно и динамика на нём не обязательно задаётся уравнениями Гамильтона.
Фазовая плоскость — координатная плоскость, в которой по осям координат откладываются какие-либо две переменные (фазовые координаты), однозначно определяющие состояние системы второго порядка. Фазовая плоскость является частным случаем фазового пространства, которое может иметь бо́льшую размерность.
В физике колебаний на оси абсцисс фазовой плоскости откладывается значения параметра x, а на оси ординат – первая производная x по времени (что, очевидно, связывает ось ординат с импульсом. См. Фазовое пространство).
Каждая точка фазовой плоскости отражает одно состояние системы и называется фазовой, изображающей или представляющей точкой.[3] Изменение состояния системы отображается на фазовой плоскости движением этой точки. След от движения изображающей точки называется фазовой траекторией. Через каждую точку фазовой плоскости проходит лишь одна фазовая траектория, за исключением особых точек. Стрелками на фазовых траекториях показывается перемещение изображающей точки с течением времени. Полная совокупность различных фазовых траекторий — это фазовый портрет. Он даёт представление о совокупности всех возможных сочетаний системы и типах возможных движений в ней. Фазовый портрет удобен для рассмотрения движений макроскопических и квантовых частиц.
