21. Коэффициенты частной корреляции, техника их расчета в двухфакторной модели

r_yx1x2=(r_yx1-r_yx2r_x1x2)/[(1-r²_yx2)(1-r²_x1x2)]^0,5

r_yx2x1=(r_yx2-r_yx1r_x1x2)/[(1-r²_yx1)(1-r²_x1x2)]^0,5

r_yx(i)=b* (σ_x(i)/σ_y)

r_yx2x1=[1 – (1-R²_yx1x2/1-r²_yx1)]^0,5

ЧКК обычно не имеет самостоятельного значения а используются для: - отбора факторов, включаемых в модель множественных связей

- при сопоставлении частных коэффициентов отбираются факторы с наибольшими значениями этих коэффициентов

ЧКК характеризуют тесноту связи м/у результатом и соответствующим фактором при устранении влияния прочих.

В двухфакторной модели бетта-коэффициенты можно найти следующим образом:

β_x1= (r_yx1-r_yx2r_x1x2)/1-r²_x1x2

β_x2= (r_yx2-r_yx1r_x1x2)/1-r²_x1x2

Отсюда же можно вывести формулы расчета частных коэффициентов корреляции

22. Оценка Значимости Уравнения Множественной Регрессии

Как обычно все начинается с H₀ гипотезы => F-критерий Фишера и t-критерий Стьюдента

F=(R²/1-R²) * (n-m-1/m) – применима только для линейных моделей

Частный F-критерий:

F_x1=(R²_yx1x2-R²_yx2/1- R²_yx1x2)*(n-m-1)/1, (делится на 1 при включении в модель 1 фактора = степени свободы)

n-число наблюдений, m – число параметров в модели без свободного члена

Таким образом оценивается значимость дополнительного включения в модель соответствующего фактора

Если F_факт> F_таб, то с вероятностью 0,95 можно утверждать, что включения фактора x₁ после x₂ целесообразно.

Зная F-критерий, можно посчитать t-критерий Стьюдента:

t_bi=(F_x(i))^0,5

Можно посчитать и без F-критерия, но грустно становится от формулы:

t_bi=b_i/m_bi, b- коэффициент чистой регрессии при х

m_b - средняя квадратическая ошибка коэф-та регрессии b

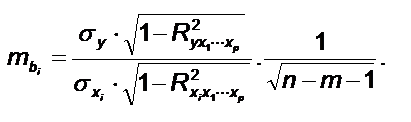
(между многочленами там знак умножить, а после просто опечатка)

25. Понятие и виды систем эконометрических уравнений.

• сложная комплексная модель элементами которой являются взаимосвязанные уравнения регрессии

Данный способ моделирования позволяет максимально приблизиться к действительным фактическим механизмам связей и взаимодействий в сложных социально- экономических системах. Это достигается благодаря включению в модель серии независимых переменных и серии зависимых переменных, при этом возможны разные виды моделей учитывающих специфику взаимосвязей рассматриваемых переменных.

Возможна ситуация, когда в отдельных уравнениях системы число х меньше чем m ( возможно если коэф. Регрессии =0)

У- зависимая переменная

Х- независимая переменная

Эндогенные переменные- наз. Зависимые переменные кот. Обычно стоят в левой части уравнения. Число уравнений = числу эндогенных переменных в данной системе.

Экзогенные переменные- аналог независимых переменных – пер-ные воздействующие на эндогенные пер-ные(у), независящие от них и не корелирующие с остатками(Е)

Лаговые пер-ные- значения включённых в модель переменных за некоторый предшествующий момент или отрезок времени. Обычно строится по текущим значениям экзогенных или эндогенных переменных.(Y_t-1, X_t-1, Y_t-2 ... )

Изменение в хар-ре фактов отражаются на следствии лишь через некоторый отрезок времени поэтому следует учесть тот отсроченный эффект влияния и для этой цели применяются лаговые переменные.

Предопределённые переменные- пер-ные кот. Точно определены к данному моменту или интервалу времени, являются экзогенными переменными ,как текущие, так и лаговые, и лаговые эндогенные переменные.

У₁= а₁₀+а₁₁х₁₁+а_13(t-₁₎x_13(t-1)+E₁

Y₂ =a₂₃+a₂₁x₂₁ +a_23(t-1)x_23(t-1)+E₂

Виды ур-ний отличаются по хар-ру озицый эндогенных переменных в системе ур-ний.

В системе независимых эконометрических уравнений эндогенные переменные никогда не зависят друг от друга. В правой части ур-ния никогда нет у. Следствие того, что ур-ние явл.независимым выступают положения: 1. Остатки (ошибки) разных ур-ний не корелируют между собой

Для построения модели т.е. расчётов коэффициентов а можно моделировать каждое ур-ние автономно с помощью методов наименьших квадратов подобно тому, как это выполняется для ур-ний множественной регрессии. Аналогичным образом автономно для каждого оценивается теснота связи и качество модели.

Система уравнений кажущихся независимыми.

Существуют неявные механизмы связи эндогенных переменных

Y₁=f(x₁,x₂,x₃)

Y₂=f(x₁,x₂,x₃₎

I y₁ - урожайность картофеля II y₁ –урожайность подсолнуха

y₂ – урожайность овса y₂ – продуктивность свиноводства

Вывод: система ур-ний с кажущейся независимыми переменными требует особого порядка построения моделей.

Рекурентные Одновременные (взаимозависимые,совместные)

Y ₁

Y ₂

Y₃

Y₄

.

.

y_n

Y ₁

Y₂

Y ₃

Y ₄

.

.

y_n

Система рекуррентных ур-ний отличается тем, что независимые переменные в правой части ур-ния являются стабильными, а зависимые-эндогенные – включаются в кажное последующее уравнение в качестве одного из факторов т.е. включаются в правую часть ур-ния ,при этом сохраняется строгая последовательность ур-ния в каждом следующем ур-ние по порядку увеличения числа у в правой части.

Пример: У₁= а₁₀+а₁₁х₁+а₁₂x₂+E₁

У₂= b₂₁y₁ +а₂₀+а₂₁х₁+а₂₂x₂+E₂

У₃= b₃₁y₁ + b₃₂y₂+а₃₀+а₃₁х₁+а₃₂x₂+E₃

…

У_n= b_n1y₁ + b_n2y₂+ … + b_nn-1y_n-1+а_n0+а_n1х₁+а_n2x₂+E_n

Св-ва:

• каждое рекуррентное ур-ние может рассматриваться как самостоятельная модель

• параметры каждого ур-ния могут определяться с помощью метода наименьших квадратов

Если система рекурентных уравнений не линейна то для нахождения параметров требуется проведение предварительной линеаризации т.е. приведение к линейной форме. Выполняется методом логарифмирования.

Пример системы рекурентных ур-ний:

У₁= а₁₀+а₁₁х₁+а₁₂x₂+E₁+a₁₃x₃

У₂= b₂₁y₁ +а₂₀+а₂₁х₁+а₂₂x₂+E₂ +a₂₃x₃

У₁- производительность труда

У₂-фондоотдача

х₁ – фондовооруженность труда

х₂ – энерговооружённость труда

х₃ –квалификация рабочих

В системе одновременных уравнений в отличие от предыдущих каждое ур-ние может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприемлем. Пример: модель динамики цены и заработной платы

У ₁= b₁₂y₂ + а₁₁х₁+ E₁

У₂= b₂₁y₁ + а₂₂х₂+а₂₃x₃+E₂

У₁- темп изменения месячной зарплаты

У₂ – темп изменения цен

х₁ -процент безработных

х₂ - темп изменения постоянного капитала

х₃ – темп изменения цен на импорт сырья