17. Натуральная и стандартизированная формы модели множественной регрессии

Параметры ур-ий множественной регрессии оцениваются Методом Наименьших Квадратов (МНК). При его применении строят систему нормальных уравнений.

Для ур-ия: y=a+ b₁x + b₂x₂ +…+b_px_p + e система нормальных ур-й имеет вид:

“ЭТО ВСЕ В СИСТЕМЕ”

Σy=na +b₁*Σx₁ +b₂* Σx₂ +…+ b_p*Σx_p

Σy*x₁=a* Σx₁ + b₁* Σx₁²+ b₂* Σx₁*x₂+…+b_p * Σx_p*x_{1 ……………………………}

Σy*x_p=a* Σx_p + b₁* Σx₁*x_p+ b₂* Σx₂*x_p+…+b_p * Σx_p²

Решение системы осуществляется методом определителей (в учебнике стр.125-126)

Иначе параметры можно определить путем построения ур-ия регрессии в стандартизированном масштабе на основе матрицы парных коэффициентов корреляции:

t_y=β₁t_x1 + … + β_pt_xp + e; где β – стандартизированные коэффициенты регрессии, t – стандартизированные переменные: 1) t_y= (y – y_ср)/σ_y 2) t_xi= (x_i – x_{i ср})/σ_xi

Применив МНК к ур-ию регрессии, получим сис-му нормальных ур-й с коэффициентами парной корреляции (стр. 128 учебника)

(18 вопрос включен – оценка параметров ур-ия множественной регрессии и их экономическая интерпретация)

Стандартизированные коэффициенты показывают на сколько сигм изменится в среднем результат, если фактор x изменится на 1 сигму при неизменном уровне других факторов.

β в отличии от коэффициентов «чистой» регрессии сравнимы между собой.

В парной зависимости стандартизированный коэффициент регрессии – линейный коэффициент корреляции r_yx

Во множественной регрессии коэффициенты «чистой» регрессии b связаны со станд. коэффициентами β: b_i=β_i (σ_y/σ_xi) β_i=b₁(σ_xi/σ_y) Следовательно, от стандартизированной формы можно переходить к ур-ию в натуральном масштабе (от t_y к y=a +b₁x₁+…+b_px_p), Параметр а: а=y_ср-b₁x_ср1 - … - b_px_{ср p}

β₁=(r_yx1- r_yx2*r_x1x2)/1-r²_x1x2 β₂=(r_yx2- r_yx1*r_x1x2)/1-r²_x1x2

По бетта коэффициентам можно сравнивать факторы по силе влияния их на результат => можно отсеивать факторы с наименьшим значением β_j

19. Показатели силы связи в модели множественной регресии в абсолютной и относительной форме

Абсолютные - показывают, на сколько единиц в среднем изменяется результативный признак при изменении рассматриваемого факторного признака на одну единицу при условии, что остальные факторы зафиксированы на среднем уровне и не меняются. (b-параметры в уравнении)

Относительные показывают, на сколько процентов в среднем меняется результативный признак при изменении рассматриваемого факторного признака на один процент при условии, что остальные факторы зафиксированы на среднем уровне и не меняются. (коэффициент Эластичности)

Э_yx(j)=b_j(x_{j ср}/y_ср)

20. Коэффициент множественной корреляции и детерминации

Практическая значимость ур-ия множественной регрессии оценивается с помощью показателя множественной корреляции (теснота связи факторов с признаком) и детерминации

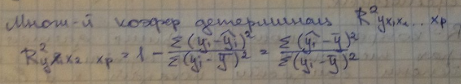
Корень из Коэффициента Детерминации – Корреляция.

Оба измеряются от 0 до 1. Чем ближе к 1, тем более тесная связь

Коэффициент детерминации показывает на сколько % вариация y обусловлена вариацией включенных в модель независимых переменных

Коэффициент Корреляции определяет меру тесноту связи (слабая-умеренная-сильная)

Вспомогательными инструментами измерения тесноты связи являются Скорректированный коэффициент множественной детерминации и Частные Коэффициенты Множественной Корреляции.

Скорректированный КМД:

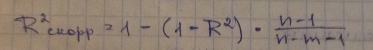
n – число наблюдений

m – число параметров при переменных X

Применяется для того чтобы не допустить возможного преувеличения тесноты связи, он содержит поправку на число степеней свободы.