5.Парная регрессия в условиях линейной связи, порядок расчетов и интерпретация параметров.

В парной регрессии спецификация модели связана с выбором вида математической функции, а в множественной- также с отбором факторов, включаемых в модель.

При построении регрессионных моделей могут использоваться как линейные, так и нелинейные функции.

Линейная модель лучше потому что:

• вариация переменных X и Y может быть весьма ограничена, и реальный эффект нелинейности их связи может не проявится.

• Аргументы- ясно, что чрезмерное внесение удобрений может привести не к росту, а к снижению урожайности, но фактически подобная ситуация маловероятна. Так что если теоретически мы должны выразить зависимость урожайности от удобрений как a+bx+cx²+E, то, вероятнее всего, вполне достаточным будет выражение y=a+bx+E.

• Ошибки измерения в переменных могут свести на нет усилия по усложнению модели. Кроме того- при грубых измерениях более эффективно простое описание связей.

Модель парной линейной связи имеет вид парной математической функции y=a+bx, где у – зависимая переменная, т.е. признак-следствие. x – независимая переменная, т.е. признак-фактор. a- свободный член уравнения, он не имеет экон интерпретации. Алгебраическая интерпретация: а=у при х=0. a только для нахождения b. b – коэффициент регрессии, он имеет твердый однозначный смысл: показывает, на сколько изменится(увелич или уменьш) y с увеличением х на 1 единицу.

Коэффициент регрессии определяет среднюю типичную тенденцию, характерную для всей совокупности единиц наблюдения. Индивидуальные данные по отдельным единицам будут отклоняться от этой общей тенденции под влиянием всех неучтенных факторов.

Так же это наклон линии регрессии или коэффициент регрессии. Он является мерой зависимости переменной y от переменной x. В линейном уравнении регрессии параметр является абсолютным показателем силы связи. Знак при коэффициенте регрессии b показывает направление связи: при b>0- связь прямая, а при b<0 – связь обратная.

Задача: анализ зависимости объема валового регионального продукта от суммы налоговых доходов консолидированного бюджета.

Формируем таблицу

Xi – сумма налоговых доходов консолид бюджета(млрд.руб.)

Yi – сумма ВРП(млрд.руб.)

Параметры уравнения регрессии определяются с помощью метода наименьших квадратов:

1)Строим систему норм уравнений

2)Решаем относительно b

3)Получаем:

Yсреднее=∑Yi/n

Xсреднее=∑Xi/n

( X*Y)среднее=(∑x*y)/n

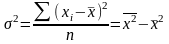
Сила связи(регрессионный анализ)

y=а+bx

a=yсреднее – b*xсреднее

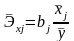
6.Парная корреляция в условиях линейной связи, порядок расчетов и интерпретация параметров.

Парный линейный коэффициент корреляции измеряет силу тесноты связи, то есть определяет долю исследуемого фактора х в совокупном воздействии всех факторов.

Задача: анализ зависимости объема валового регионального продукта от суммы налоговых доходов консолидированного бюджета.

Формируем таблицу

Xi – сумма налоговых доходов консолид бюджета(млрд.руб.)

Yi – сумма ВРП(млрд.руб.)

Параметры уравнения регрессии определяются с помощью метода наименьших квадратов:

1)Строим систему норм уравнений

2)Решаем относительно b

3)Получаем:

Yсреднее=∑Yi/n

Xсреднее=∑Xi/n

( X*Y)среднее=(∑x*y)/n

Теснота связи(корреляционный анализ)

парный линейный коэффициент корреляции

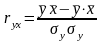
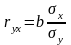
-1<r_yx <1

Чем ближе к нулю, тем меньше зависимость

Шкала значений коэффициента корреляции:

• До 0,3 связь слабая

• 0 ,3-0,5 связь умеренная

• 0,5-0,7 связь заметная

• 0,7-0,9 связь высокая

• 0,9-1,0 связь весьма высокая, близкая к функциональной

Допустим r²_xy =0,85 , тогда можно сделать вывод о том,что на 0,85 общая вариация y обусловлена вариацией x. На 85% доля расходов на питание (к примеру) обусловлена ср.зар.платой (тоже к примеру) и на 15% - прочими неучтенными факторами.

Чем ближе к r²xy 1, тем лучше (тем меньше доля остаточной функции)

r²_xy - коэффициент детерминации, показывает, на сколько % вариация у объясняется вариацией х и сколько % приходится на долю прочих факторов, не учитываемых в регрессии.