31. Порядок расчета и интерпретация параметров линейного уравнения тренда

Параметры линейного уравнения тренда определяются по обычным МНК используя в качестве независимой переменной время t=1,2,…,n, а в качестве зависимой переменной – фактические уровни ВР y_t

Оценка параметров производится по обычным формулам:

y=a+bt

параметр b≈ _{y (}средний абсолютный прирост уровней ряда₎

_{( y=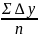 = ) * - после сокращения как раз мы получим}

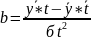
Параметры линейного тренда интерпретируют так:

а - исходный уровень временного ряда в момент времени t = 0;

b — средний за период абсолютный прирост уровней ряда.

36. Прогнозирование на основе модели тренда

Пусть требуется дать прогноз уровня временного ряда на период (n +1). Точечный прогноз значения уровня временного ряда х _n +1 в аддитивной модели есть сумма трендовой компоненты и сезонной компоненты (соответствующей i –ому сезону прогноза):  = T_n +1+S_i . 

В мультипликативной модели – произведение трендовой и сезонной компоненты = T_n +1* S_i Для построения доверительного интервала прогноза нужно рассчитать среднюю ошибку прогноза:  m ^р =  ,  где h- число параметров в уравнении тренда;  t^yp – значение условной переменной времени для периода прогнозирования.  Затем рассчитаем предельную ошибку прогноза: D ^р =t_a · m_р,  где t_a- коэффициент доверия, определяемый по таблицам Стьюдента по уровню значимости α и числу степеней свободы равным ( n-h).  Окончательно получим:  ( - D^р;  + D ^р).

37.Модели тренда на основе нелинейных функций

Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:

• линейный тренд: ў_t = a+b·t;

• гипербола: ў_t = a+b/t;

• экспоненциальный тренд: ў = e^a+bt (или ў=a·b^t);

• степенная функция: ў = a·t^b;

• полиномы различных степеней: ў_t = a + b₁·t + b₂·t² + ... + b_m·t^m.

Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время t=1,2,...,n, а в качестве зависимой переменной – фактические уровни временного ряда ў_t. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.

Наиболее простую экономическую интерпретацию имеет линейная функция y = a+b·t

а – начальный уровень временного ряда в момент времени t = 0;

b – средний за период абсолютный прирост уровней ряда.

Параметры а и b находятся по формулам:

Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени.

Выбор наилучшего уравнения в случае, когда ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации и средней ошибки аппроксимации. Этот метод легко реализуется при компьютерной обработке данных.