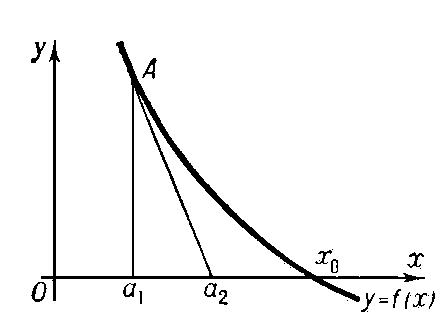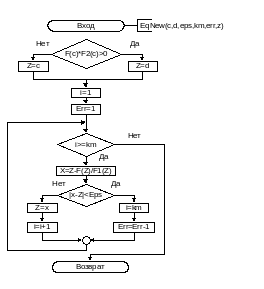
Подпрограмма-процедура EqHord предназначена нахождения корня нелинейного уравнения.

Список формальных параметров: C, D, Eps, Km, Err, Z.

Входные данные:

5. C – верхняя граница интервала изоляции корня, тип – вещественный;

6. D – нижняя граница интервала изоляции корня, тип – вещественный;

7. Eps – погрешность вычисления корня, тип –вещественный;

8. Km – предельно допустимое количество повторов циклов, тип-целый;

Выходные данные:

3. Err – признак ошибки, тип-целый;

4. Z – корень нелинейного уравнения, тип – вещественный.

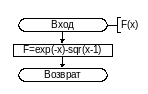
Подпрограмма-функция F предназначена для вычисления значения функции F

Список формальных параметров: Х.

Входные данные:

1.Х – аргумент функции, тип – вещественный.

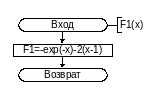
Подпрограмма-функция F1 предназначена для вычисления значения функции F1(первой производной от функции F)

Список формальных параметров: Х.

Входные данные:

1.Х – аргумент функции, тип – вещественный.

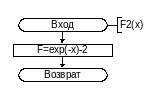
Подпрограмма-функция F2 предназначена для вычисления значения функции F2(второй производной от функции F)

Список формальных параметров: Х.

Входные данные:

1.Х – аргумент функции, тип – вещественный.

Текст подпрограмм

1.Подпрограммы-функции F,F1,F2

1.1 Подпрограмма – функции F

{Текст подпрограммы – функции F}

Function F(X:real):real;

begin

F:=exp(-x)-(sqr(x-1));

end;

1.2 Подпрограмма – функции F1

{Текст подпрограммы – функции F1}

Function F1(X:real):real;

begin

F1:=-exp(-x)-2* (x-1);

end;

1.3 Подпрограмма – функции F2

{Текст подпрограммы – функции F2}

Function F2(X:real):real;

begin

F2:=exp(-x)-2;

end;

2.Текст подпрограммы – процедуры EqHord

{Teкст процедуры нахождения корня нелинейного уравнения методом хорд}

Procedure Eqhord (c,d,eps:real; km:integer; var err:integer; var z:real);

var

i:integer;

begin

z:=(d-c)/(F(d)-F(c))

if F(c)*F2(c)>0 then

Q=c else

Q=d;

i:=1;

err:=1;

repeat

x:=Q-F(Q)*z

if |x-Q|>Eps then

begin

Q:=x;

i:=i+1;

end else

begin

i:=km;

Err:=Err-1;

end;

until i>=km

end.

10.1.3.3.Метод Ньютона Теоритические сведения.

Метод ньютона – это метод приближённого нахождения корня x₀ уравнения f (x) = 0, называемый также методом касательных. Н. м. состоит в том, что по исходному («первому») приближению х = a₁ находят второе (более точное), проводя касательную к графику (см. рис.) у = f (x) в точке А [а₁ f (a₁)] до её пересечения с осью Ox; точка пересечения х = a₁ — f (a₁)/f’(a₁) и принимается за новое значение a₂. корня. Повторяя в случае необходимости этот процесс, получают всё более и более точные приближения a₂, a₃,... корня x₀ при условии, что производная f’(x) монотонна и сохраняет знак на сегменте, содержащем x₀. Ошибка ε₂ = x₀ —a₂ нового значения a₂ связана со старой ошибкой ε₁ = x₀ — a₁ формулой  f (x) в некоторой точке x, лежащей между x₀ и a₁. Иногда рекомендуется Н. м. применять одновременно с к.-л. другим способом, например с Линейного интерполирования методом. Н. м. допускает обобщения, которые позволяют применять его для решения уравнений F (x) = 0 в нормированных пространствах (F— оператор в этом пространстве), в частности для решения систем уравнений и функциональных уравнений. Метод разработан И. Ньютоном в 1669.