7.Арифметические циклы

В арифметических циклах число повторений заранее определено. Оно может быть задано явно (массив N элементов) или вычислено по известному диапазону изменения параметров цикла.

7.1. Табулирование функций

-это задача вычисления таблицы значений функций при изменении аргумента и параметра. Если формульная зависимость включает аргумент и параметр, то внутренний цикл отражает значение аргумента, а внешний – параметра. Если схема алгоритма выполняется в виде программы, то она должна снабжаться таблице обозначения переменных, а если в виде подпрограмм, то описанием формальных параметров.

7.2 Накопление суммы. Последовательное умножение.

Составить схему алгоритма для вычисления или нахождения среднего значения величин «a» и «t».

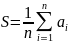
Р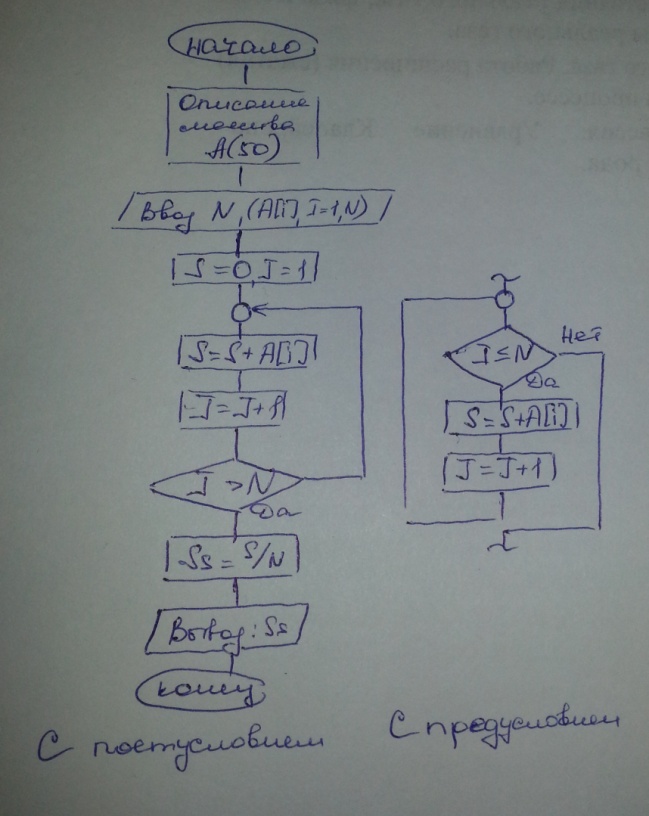 ешение

Таблица значения элементов:

Условие	Схема	Обозначение
N	N	Количество элементов массива, тип-целый
A	A	Массив значений, тип-вещ.
S	S	Сумма
Ss	Ss	Среднее значение
I	I	Счетчик циклов

Формула накопления слева и справа стоит одна и та же переменная.

Аналогичным повторением суммы выполняется возведение в целую степень как повторение умножения(последовательное умножение)

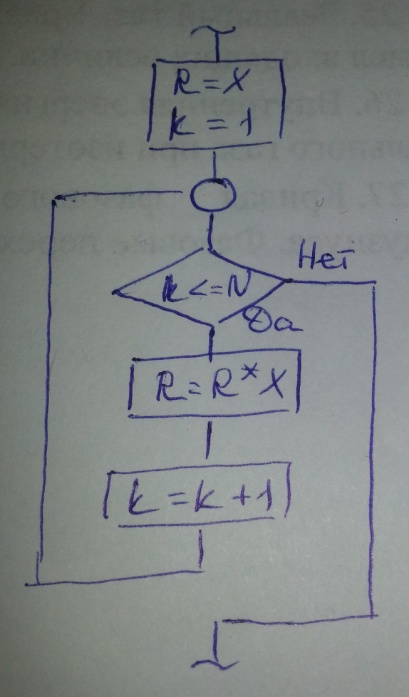
7.4. Обработка массивов данных

Составить схему алгоритма для нахождения минимального значения двумерного массива и его координат матрицы заданного размера. Оформим в виде подпрограммы.

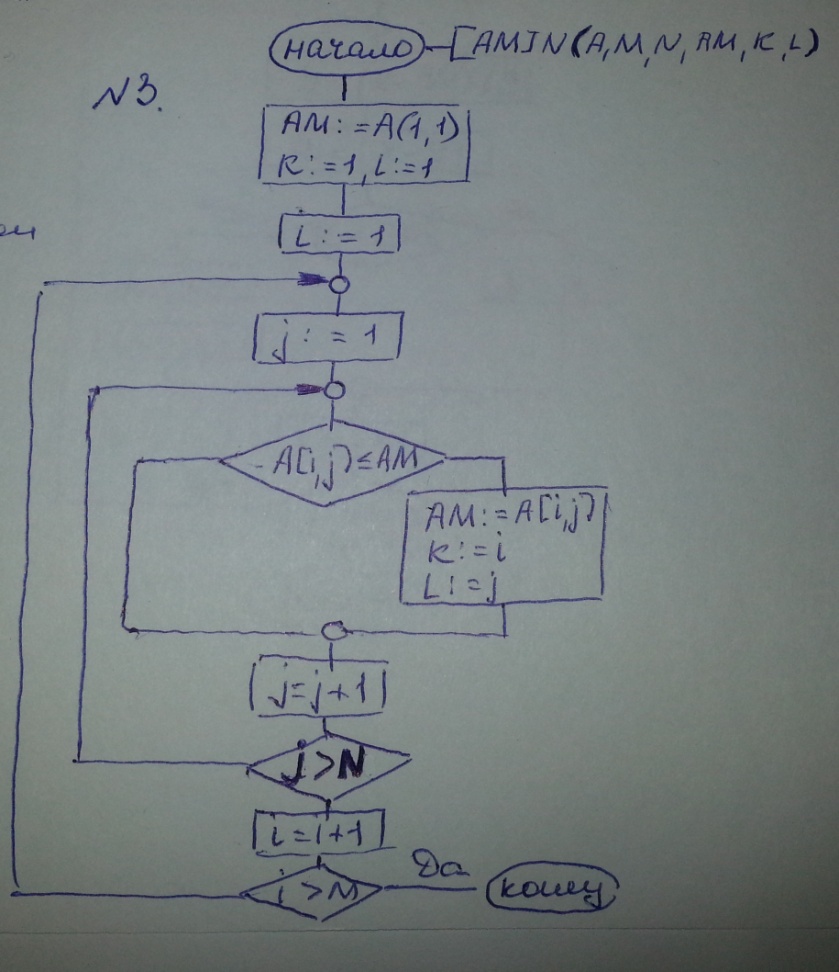
Подпрограмма AMIN предназначена для нахождения минимального элемента двумерного массива и его координат в матрице заданной погрешности.

Список формальных параметров: A, M, N, AM, K, L

Входные параметры: A, M, N

A – двумерный массив, тип- действительный

M – количество строк матрицы, тип – целый

N – количество столбцов матрицы, тип – целый

Выходные параметры: AM, K, L

AM – минимальный элемент, тип – действительный

K – номер строки минимального элемента, тип – целый

L – номер столбца минимального элемента, тип – целый

7.3 Вычисление суммы ряда при заданном числе членов разложения

Составить схему алгоритма для вычисления суммы ряда.

Общий подход вычисления функции состоит в разложении этой функции в ряд Тейлора, Макларена, Чебышева.

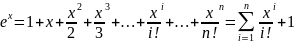
Ряд – это сумма бесконечного числа слагаемых(членов разложения), каждый из которых зависит от предыдущего и связан с ним рекуррентной зависимостью, т.к. количество членов этого ряда бесконечно, то в численных методах используют ограниченной количество членов, которое может быть задано явно или определяться допустимой погрешностью как будет показано далее. Найдем рекуррентную формулу:

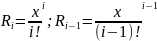
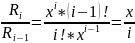
С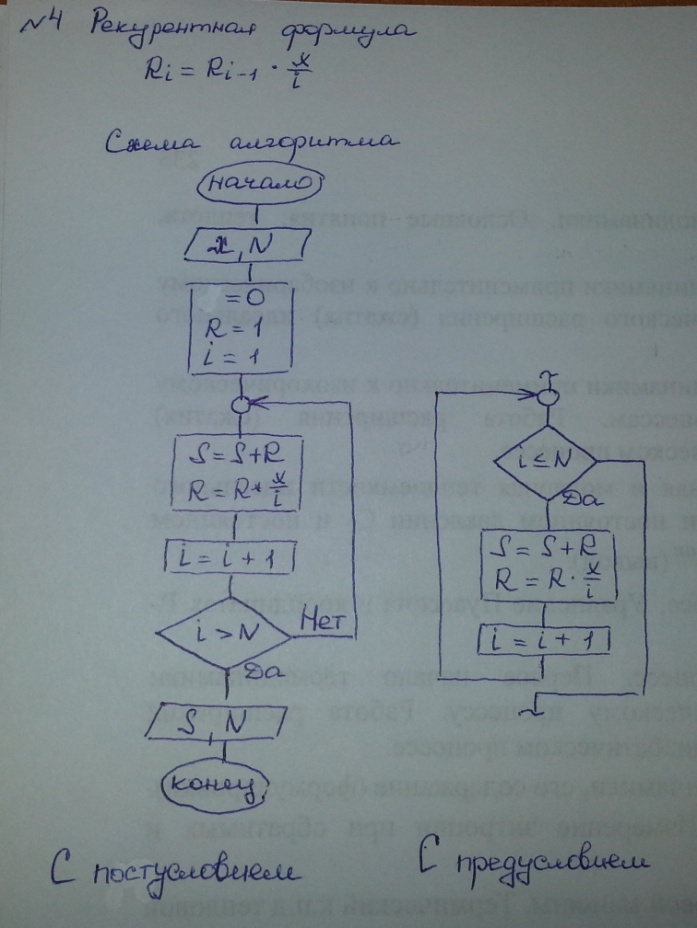 писок формальных параметров

Условие	Схема	Что обозначает
X	X	Аргумент, т- в
N	N	Число слагаемых, т-ц
	S	Сумма ряда , т-в
	R	Общий член ряда, т – в
	i	Текущий номер элемента, т-ц