Вопрос 16

Частичные последовательности. Пусть дана некоторая по­следовательность

Рассмотрим, наряду с нею, какую-либо извлеченную из нее частич­ную* последовательность

где есть некоторая последовательность возрастающих на­туральных чисел:

Здесь роль номера, принимающего подряд все натуральные зна­чения, играет уже не , а ; же представляет собой функцию от , принимающую натуральные значения и, очевидно, стремящуюся к бесконечности при возрастании .

Если последовательность (1) имеет определенный предел {конечный или нет), то тот же предел имеет и частичная последовательность (2).

Если же для последовательности (1) нет определенного предела, то это не исключает возможности существо­вания предела для какой-либо частичной последовательности.

Пусть, например, ; предела эта переменная не имеет; Если же заставить п пробегать лишь одни нечетные или одни четные значения, то частичные последовательности

будут иметь пределом, соответственно, число или

В случае неограниченной последовательности (1) иной раз оказывается невозможным выделение частичной последовательности (2), имеющей конечный предел [так будет, если сама последователь­ность (1) стремится к ]. Наоборот, для ограниченной после­довательности имеет место следующее утверждение, принадлежащее Больцано и Вейерштрассу¹):

Нижним пределом последовательности называется наименьший частичный предел последовательности.

Верхним пределом последовательности называется наибольший частичный предел последовательности.

Условие существования предела последовательности эквивалентно условию равенства верхнего и нижнего пределов этой последовательности.

Вычисление верхнего и нижнего пределов последовательности сводится к тому, что выделяют сходящиеся подпоследовательности и сравнивают их пределы.

Пример 29. Пусть дана последовательность x_n = n^(-1)n, n N. Так как x_2k = 2k, x_2k+1= 1/(2k+1), то lim_nx_n = +. и lim_nx_n = 0.

Вопрос 17

Если последовательность (1) имеет определенный предел {конечный или нет), то тот же предел имеет и частичная последовательность (2).

Если же для последовательности (1) нет определенного предела, то это не исключает возможности существо­вания предела для какой-либо частичной последовательности.

Пусть, например, ; предела эта переменная не имеет; Если же заставить п пробегать лишь одни нечетные или одни четные значения, то частичные последовательности

будут иметь пределом, соответственно, число или

В случае неограниченной последовательности (1) иной раз оказывается невозможным выделение частичной последовательности (2), имеющей конечный предел [так будет, если сама последователь­ность (1) стремится к ]. Наоборот, для ограниченной после­довательности имеет место следующее утверждение, принадлежащее Больцано и Вейерштрассу²):

Вопрос 18 Основные элементарные функции. Элементарные функции

1. постоянная  ;

2. степенная , задано;

3. показательная ;

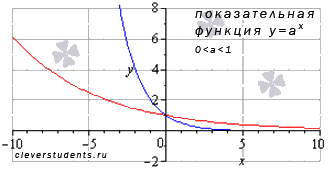
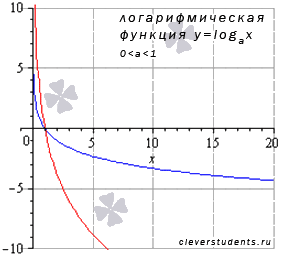
4. логарифмическая ;

5. тригонометрические  ;

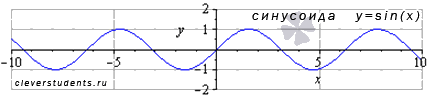
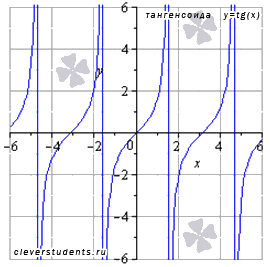
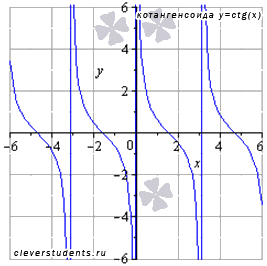
6. обратные тригонометрические

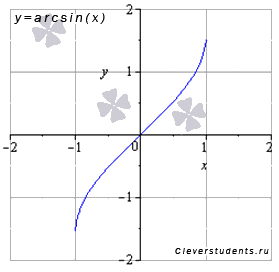
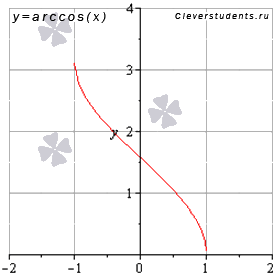
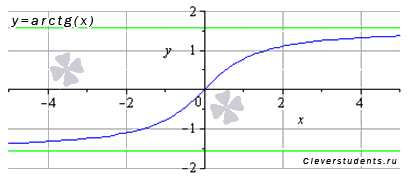
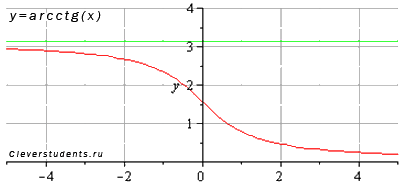
Область определения функции это когда X может быть!!