[Править]Лемма о вложенных отрезках и полнота (непрерывность) поля вещественных чисел

Основная статья: Непрерывность множества действительных чисел

Лемма о вложенных отрезках тесно связана с непрерывностью (полнотой) поля вещественных чисел. Так, вышеприведенное доказательство леммы существенно опиралось на аксиому непрерывности. Можно показать, что если упорядоченное поле не является непрерывным, то принцип вложенных отрезков может не иметь места. Например, если взять поле рациональных чисел, которое не является непрерывным, и рассмотреть последовательность вложенных отрезков

концы которых — суть десятичные приближения иррационального числа с недостатком и избытком соответственно с точностью , то окажется, что у этой системы вложенных отрезков нет общей точки.

Более того, можно показать, что принцип вложенных отрезков является одной из эквивалентных формулировок непрерывности поля (и поэтому его называют принципом непрерывности по Кантору). Точнее, имеет место следующее предложение^[2]. Для всякогоархимедова упорядоченного поля из принципа вложенных отрезков вытекает непрерывность этого поля.

Вопрос 14 Способы определения

Число e может быть определено несколькими способами.

Через предел:

(второй замечательный предел).

Как сумма ряда:

или .

Через определённый интеграл:

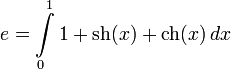
Как единственное число a, для которого выполняется

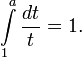
Как единственное положительное число a, для которого верно

Свойства

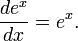Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения 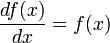является функция 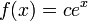, где c — произвольная константа.
Число e иррационально и даже трансцендентно. Его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.

Число е

Число e выражается через предел следующим образом:

Это число является трансцендентным и приблизительно равно 2,718281828... (2.7, затем два раза год рождения Л.Н.Толстого). Выполнив подстановку , где , получим альтернативную формулу для данного предела:

Здесь мы имеем дело со степенными выражениями, когда и основание и степень стремятся к числу a (или к бесконечности). Во многих случаях такие пределы удобно вычислять, предварительно логарифмируя функцию под знаком предела.

Пример 1

Вычислить предел .