
- •Вопрос 1 Множество рациональных чисел
- •Вопрос 2
- •Аксиома непрерывности
- •Вопрос 3 Непрерывность по Дедекинду
- •Вопрос 4
- •Используемые определения
- •[Править]Определения
- •[Править]Замечание
- •Вопрос 5 Десятичная запись вещественного числа
- •Вопрос 6
- •Вопрос 7
- •Вопрос 8 Вещественный логарифм
- •Вопрос 9
- •Определение
- •Вопрос 10 Свойства [править]Арифметические свойства
- •[Править]Свойства сохранения порядка
- •Вопрос 11
- •Вопрос 12 Предел суммы, разности, произведения и частного двух последовательностей
- •Вопрос 13 Предел монотонной ограниченной последовательности. Существование корня степени из вещественного числа. Число
- •II. Число (число Эйлера, число Непера)
- •[Править]Лемма о вложенных отрезках и полнота (непрерывность) поля вещественных чисел
- •Вопрос 14 Способы определения
- •Свойства
- •Вопрос 15
- •Вопрос 16 Частичный предел последовательности
- •Определение
- •[Править]Обозначения
- •[Править]Примеры
- •[Править]Свойства
- •Вопрос 17
- •Степенная функция.
- •Степенная функция с нечетным положительным показателем.
- •Степенная функция с нечетным отрицательным показателем.
- •Степенная функция с четным положительным показателем.
- •Степенная функция с четным отрицательным показателем.
- •Степенная функция с рациональным показателем.
- •Логарифмическая функция.
- •Тригонометрические функции, их свойства и графики.
- •Обратные тригонометрические функции графики.
- •Вопрос 19
- •Вопрос 20
- •Математический анализ
- •Вопрос 21
- •Вопрос 22
- •Вопрос 23
- •Функция Дирихле
- •Вопрос 24
- •Вопрос 25 Предел суммы, разности, произведения и частного двух последовательностей
- •Вопрос 26
- •Вопрос 27 Первый замечательный предел
- •Вопрос 28
- •Второй замечательный предел
- •Вопрос 29
- •Вопрос 30 Непрерывность функции в точке
- •Вопрос 31
- •Вопрос 32
- •Вопрос 33
- •Вопрос 34
- •Вопрос 35
- •Вопрос 36
- •Вопрос 37 § Производная функции в точке
- •Вопрос 38
- •Вопрос 39 Производная суммы и разности
- •Производная произведения
- •Производная частного
- •Вопрос 40 Производная сложной функции
- •Вопрос 41 Дифференциал функции
- •Связь между производной и дифференциалом
- •Правила дифференцирования
- •Вопрос 42
- •Вопрос 43 Применение дифференциала в приближенных вычислениях
- •Вопрос 44
- •Вопрос 45
- •Вопрос 46
- •Вопрос 47
Вопрос 37 § Производная функции в точке
Определение
приращения аргумента
|
Приращением
аргумента
функции
|
Определение
приращения
|
Приращением
функции
,
соответствующим
приращению аргумента
в точке
называется разность
между
значением функции в точке
|
Определение производной функции в точке |
Пусть функция определена в некоторой окрестности точки . Предел отношения приращения функции в этой точке (если
он существует) к приращению
аргумента, когда
Обозначается производная в точке одним из следующих способов:
Таким образом,
|
Вопрос 38
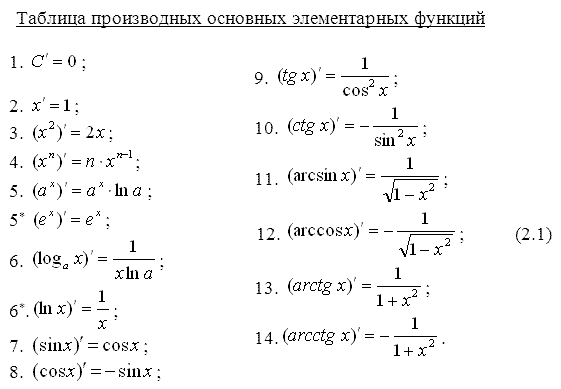
Таблицу производных желательно выучить наизусть.
Нахождение производных многих других элементарных функций (более сложных, не входящих в эту таблицу) осуществляется на основе следующих правил вычисления производных (правил дифференцирования функций):
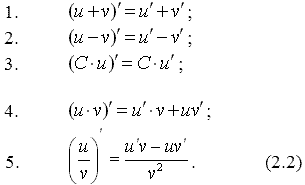
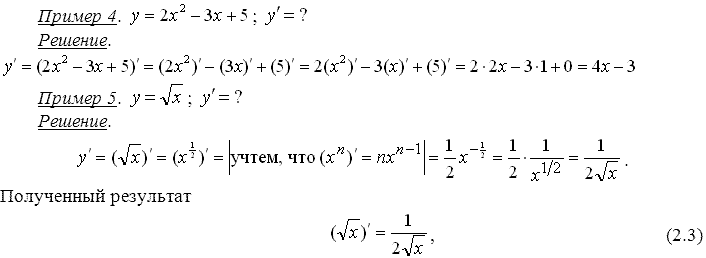
Вопрос 39 Производная суммы и разности
Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:
(f + g)’ = f ’ + g ’
(f − g)’ = f ’ − g ’
Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.
Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.
Задача. Найти производные функций: f(x) = x2 + sin x; g(x) = x4 + 2x2 − 3.
Решение. Функция f(x) — это сумма двух элементарных функций, поэтому:
f ’(x) = (x2 + sin x)’ = (x2)’ + (sin x)’ = 2x + cos x;
Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры):
g ’(x) = (x4 + 2x2 − 3)’ = (x4 + 2x2 + (−3))’ = (x4)’ + (2x2)’ + (−3)’ = 4x3 + 4x + 0 = 4x · (x2 + 1).
Ответ: f ’(x) = 2x + cos x; g ’(x) = 4x · (x2 + 1).
Производная произведения
Математика —
наука логичная, поэтому многие считают,
что если производная суммы равна
сумме производных, то производная
произведения равна
произведению производных.
А вот фиг вам! Производная
произведения считается совсем по другой
формуле. А именно:
(f · g) ’ = f ’ · g + f · g ’
Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.
Задача. Найти производные функций: f(x) = x3 · cos x; g(x) = (x2 + 7x − 7) · ex.
Решение. Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:
f ’(x) = (x3 · cos x)’ = (x3)’ · cos x + x3 · (cos x)’ = 3x2 · cos x + x3 · (− sin x) = x2 · (3cos x − x · sin x)
У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g ’(x) = ((x2 + 7x − 7) · ex)’ = (x2 + 7x − 7)’ · ex + (x2 + 7x − 7) · (ex)’ = (2x + 7) · ex + (x2 + 7x − 7) · ex = ex · (2x + 7 + x2 + 7x −7) = (x2 + 9x) · ex = x(x + 9) · ex.
Ответ: f ’(x) = x2 · (3cos x − x · sin x); g ’(x) = x(x + 9) · ex.
Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.

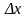
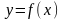 называется разность между значением
аргумента в точке
называется разность между значением
аргумента в точке
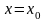 и любой другой точке из некоторой
окрестности точки
и любой другой точке из некоторой
окрестности точки
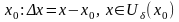 .
.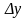 функции
функции
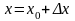 и в точке
и в точке
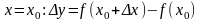 .
.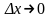 ,
называется производной функции
в точке
.
,
называется производной функции
в точке
.
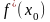 ,
или
,
или
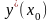 ,
или
,
или
 ,
,
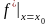 .
.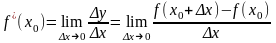 .
.