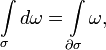Теорема Стокса
Материал из Википедии — свободной энциклопедии
(перенаправлено с «Формула Стокса»)
Теорема Стокса — одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса.
Общая формулировка
Пусть
на ориентируемом
многообразии 
размерности 
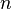заданы
ориентируемое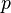 
-мерное подмногообразие 
и дифференциальная
форма
степени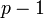 
класса 
(
).
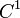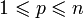Тогда, если граница подмногообразия 
положительно
ориентирована, то
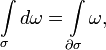
где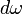 
обозначает
внешний дифференциал формы
.
Теорема распространяется на линейные комбинации подмногообразий одной размерности, так называемые цепи. В этом случае формула Стокса реализует двойственность между когомологией де Рама и гомологией циклов многообразия .
Формула Ейлера - співвідношення, що пов'язує комплексну експоненту з тригонометричними функціями. Названа на честь Леонарда Ейлера, який її запропонував.
Формула
Ейлера стверджує, що для будь-якого дійсного
числа 
виконується
рівність:
,
де 
— основа
натурального логарифма,
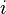— уявна
одиниця.
Формула залишається вірною також для комплексного аргументу .
Відома тотожність Ейлера, що пов'язує п'ять фундаментальних математичних констант:
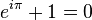
є
частковим випадком формули Ейлера
при 
.