1.6. Свойства математического ожидания.
1.
Если случайная величина
является постоянной («неслучайной»)
величиной:
,
то есть имеет закон распределения
|
|
|
|
то
,
или
.
Доказательство.
По определению
.
▄
2.
Постоянный
множитель можно выносить за знак
математического ожидания:
.
Доказательство. Ограничимся случаем конечного множества значений. Пусть закон распределения имеет вид:
.
Рассмотрим два возможных случая.
1)
.
Тогда
имеет закон распределения
|
|
|
|
так
что
,
и также
.
2)
.
Тогда условия
и
равносильны, и поэтому
;
.
Следовательно, закон распределения закон распределения случайной величины имеет вид:
.
Поэтому
.
▄
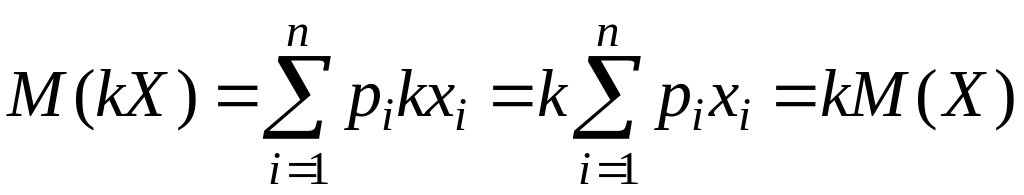3. Теорема сложения для математического ожидания.
Пусть
случайные величины
и
имеют математические ожидания
и
.
Тогда
.
Доказательство. Ограничимся случаем конечного множества значений. Пусть законы распределения для и имеют вид:
;
.
Случайная
величина
принимает
значений вида
,
где
.
Ограничимся для простоты случаем, когда
все эти значения различны. Пусть
—вероятности указанных значений. Тогда
.
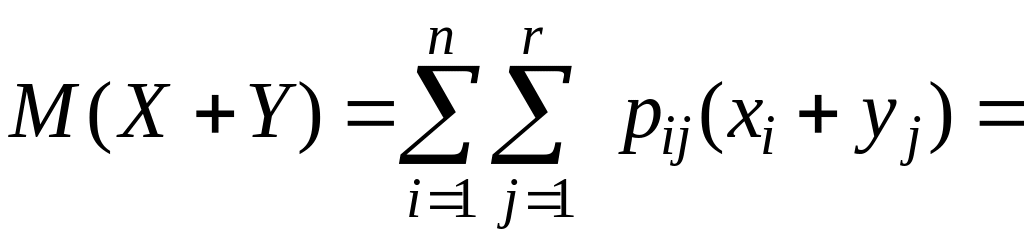
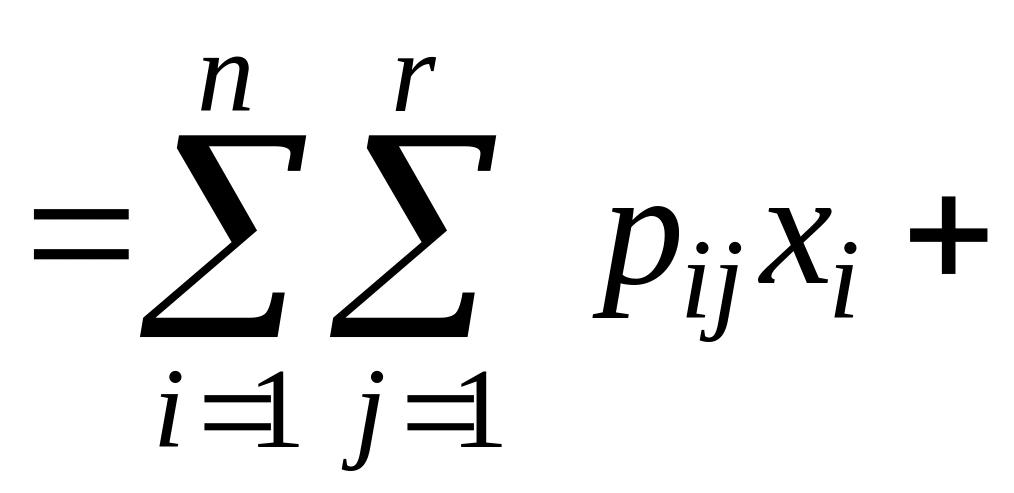
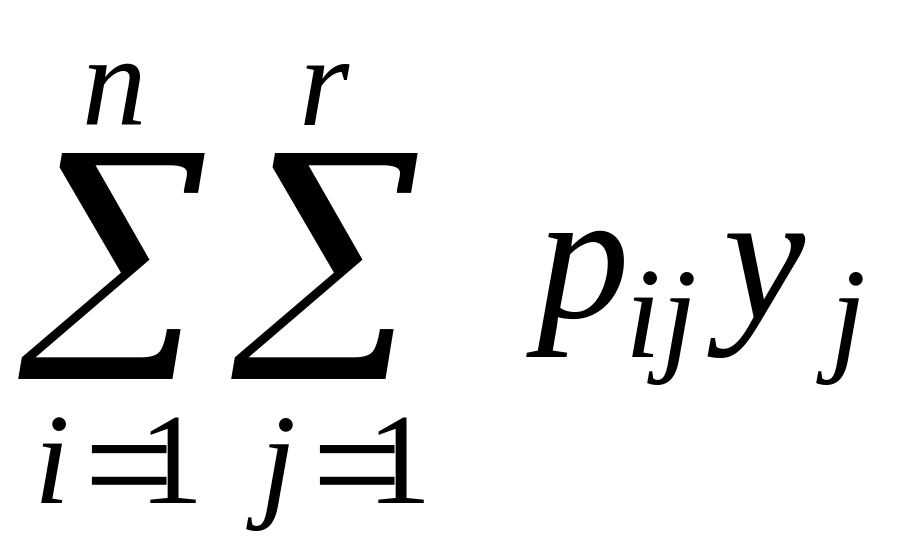Производя
в каждой из двойных сумм группировку
слагаемых и вынося за знак внутренней
суммы общий множитель (
и
,
соответственно), получаем:
.
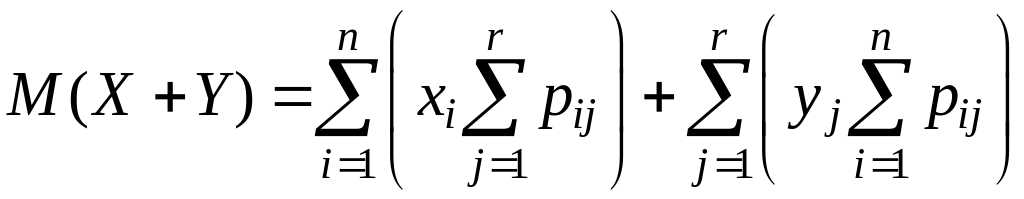Убедимся
теперь, что
.
Для этого введем события:
;
;
; … ;
.
События
,
а значит, и
попарно несовместны, поэтому (сумма
вероятностей событий равна вероятности
их суммы)
.
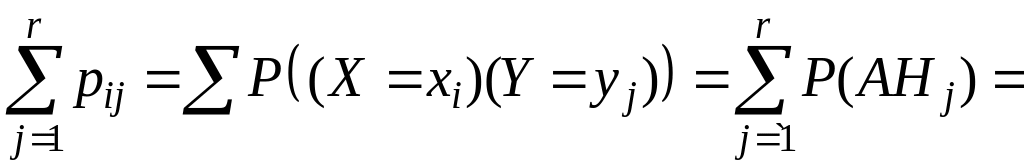
Аналогично
.
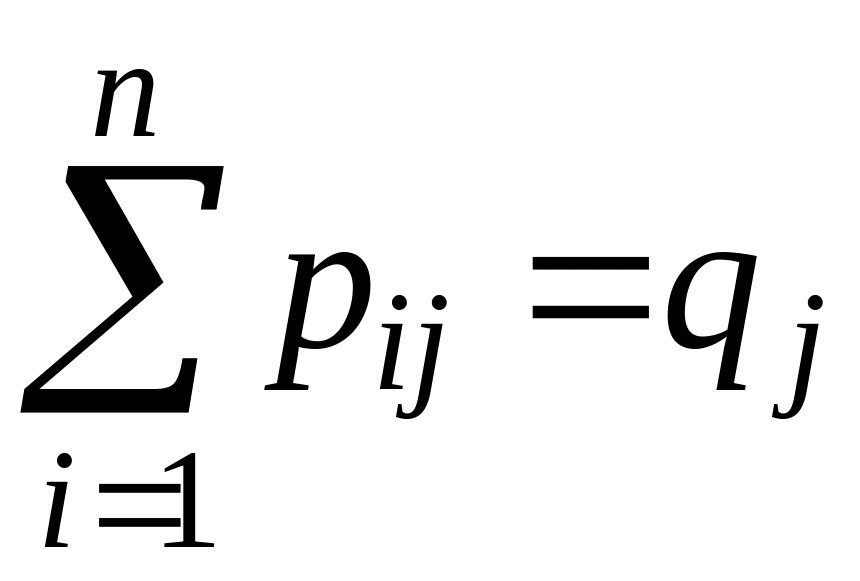Тогда
.
▄
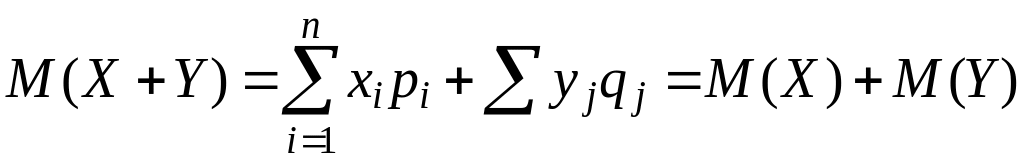4. Теорема умножения для математического ожидания.
Определение.
1.
Случайные величины
называются независимыми,
если для любых промежутков
независимы в совокупности события
,
,…,
.
2.
Случайные величины
, образующие бесконечную последовательность,
называются независимыми,
если для любого натурального
любые
случайных величин этой последовательности
независимы.
Замечание.
В частности, если
и
независимы, то для любых чисел
и
:
.
Теорема. Пусть случайные величины и независимы и имеют математические ожидания и . Тогда
.
Доказательство. Ограничимся случаем конечного множества значений. Пусть законы распределения для и имеют вид:
;
.
Случайная
величина
принимает
значений вида
,
где
.
Ограничимся для простоты случаем, когда
все эти произведения различны. Обозначим
через
вероятности этих значений. Тогда,
поскольку вероятность произведения
независимых событий равна произведению
их вероятностей,
.
Далее,
.
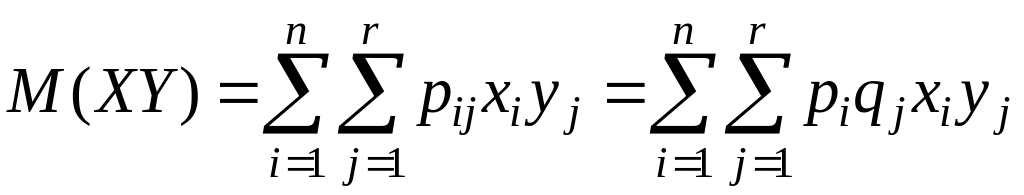Производя
в двойной сумме группировку слагаемых
и вынося за знак внутренней суммы общий
множитель
,
получаем:
.
▄
1.7. Дисперсия дискретной случайной величины
Рассмотрим следующий пример. Пусть случайные величины и имеют следующие законы распределения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нетрудно
проверить, что они имеют равные
математические ожидания:
.
В то же время рассеивание значений
вокруг математического ожидания у
явно больше, чем у
.
Это рассеивание выражается отклонениями
реализованных значений от математического
ожидания, то есть разностями
и
,
соответственно.
Определение.
Пусть у случайной величины
существует математическое ожидание
.
Случайная величина
со значениями
называется отклонением
(от
математического ожидания).
Если при большом числе реализаций случайной величины просуммировать полученные отклонения, то их значения разных знаков в значительной степени погашают друг друга, и такая сумма не может служить мерой рассеивания значений случайной величины вокруг математического ожидания. Для того чтобы избежать подобного взаимного погашения, отклонения перед суммированием возводят в квадрат.
Определение. Пусть у случайной величины существует математическое ожидание . Ее дисперсией называется число
,
(4)
то есть математическое ожидание квадрата отклонения.
Статистический смысл дисперсии:
Дисперсия служит мерой рассеивания значений случайной величины вокруг математического ожидания.
Общее определение дисперсии принимает применительно к дискретной случайной величине следующий вид:
1) Если является дискретной случайной величиной с конечным множеством значений и законом распределения
,
то отклонение имеет закон распределения
,
и, в соответствии с определением математического ожидания:
.
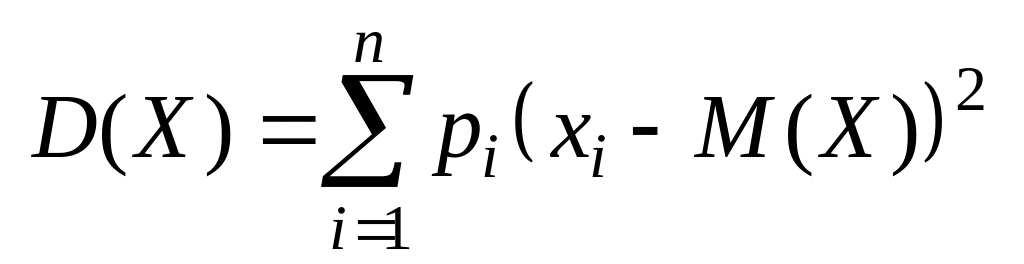(5)
2) Если является дискретной случайной величиной с бесконечным множеством значений и законом распределения
,
то
.
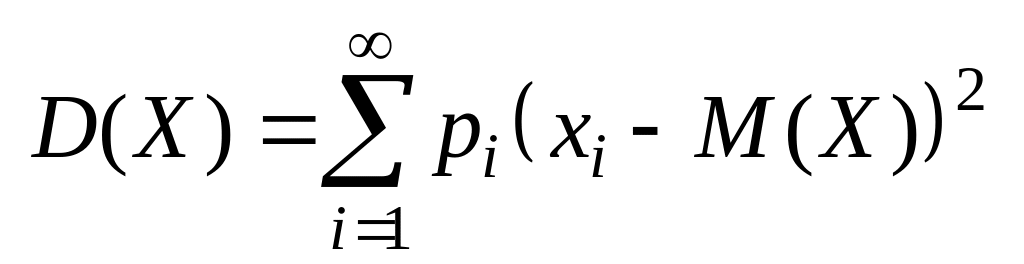(6)
Если ряд в правой части (6) расходится, то считают, что дисперсия не существует.
Замечание. Если у случайной величины не существует математического ожидания, то понятие дисперсии для нее не вводится.
Пример. 1. Пусть закон распределения имеет вид:
|
|
|
|
|
|
|
|
Вычисление дисперсии предполагает предварительное вычисление математического ожидания:
.
Далее,
.
2. Для приведенных в начале этого параграфа законов распределения получаем:
;
;
.
Среднее
квадратическое отклонение. В
случае, когда случайная величина
имеет размерность (метры, килограммы и
т. п.), размерность дисперсии
равна квадрату размерности
.
Поэтому наряду с дисперсией в качестве
меры рассеивания значений случайной
величины вокруг математического ожидания
применяют также арифметический квадратный
корень из дисперсии. Последний уже имеет
размерность, совпадающую с размерностью
.
Определение. Средним квадратическим отклонением случайной величины , называется число
.