Свойства функции распределения
1.
Для любых
и
выполняется неравенство:
.
Это следует из общих свойств вероятности случайного события ([13], п. 3.2).
2. Функция является неубывающей по каждому аргументу:
при
:
;
при
:
.
Рис. 10.
2. Функция является неубывающей по каждому аргументу:
при : ;
при : .
Доказательство. Пусть, например, . Тогда
— сумма несовместных событий. Следовательно
,
(31)
откуда
,
так как последнее слагаемое в (31), будучи
вероятностью случайного события,
неотрицательно. ▄
3. Поведение функции распределения на бесконечности:
;
;
;
.
(без доказательства).
4.
Если
– функция распределения двумерной
случайной величины
,
а
— функции распределения составляющих
и
,
то
.
(без доказательства).
Определение.
Функции распределения
и
составляющих двумерной случайной
величины называются частными
распределениями.
5. Вероятность попадания случайной точки в полосу (рис. 11):
;
(32)
.
(33)
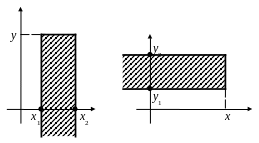
Рис.11.
Доказательство. Докажем, например, первое равенство. Событие
— сумма попарно несовместных событий. Переходя к вероятностям, получаем:
,
откуда следует нужное равенство. ▄
6. Вероятность попадания случайной точки в прямоугольник (рис. 12):
EMBED Word.Picture.8
Рис.12.
.
(34)
Доказательство. Имеет место равенство случайных событий (рис.13):
— сумма несовместных событий. Переходя к вероятностям, получаем:
P
=
.
Обе
вероятности в правой части – это
вероятности попадания в соответствующие
полосы. Применяя к ним формулу (32) при
и
соответственно, получаем требуемое
равенство (34). ▄
Рис.13.
4.2. Дискретные двумерные случайные величины
Определение. Двумерная случайная величина называется дискретной, если дискретными являются обе ее составляющих и .
Пусть законы распределения составляющих имеют вид:
и
.
Обозначим через
вероятность:
.
Закон
распределения двумерной случайной
величины имеет вид
,
причем, как и в одномерном случае,
выполняется равенство:
.
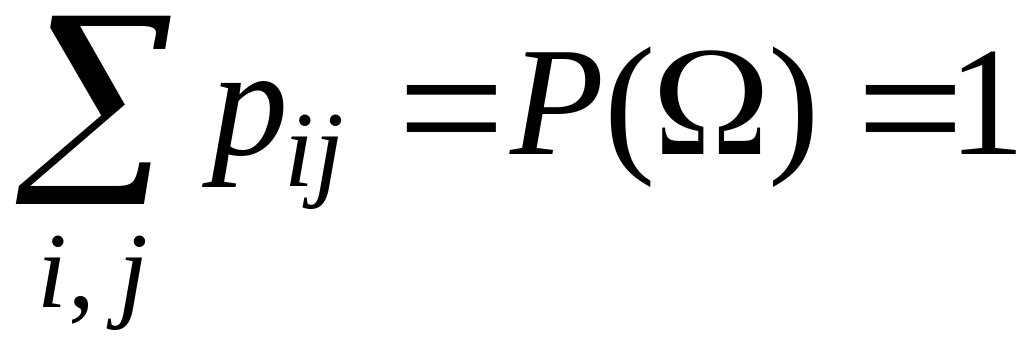Если составляющие и независимы, то по теореме умножения:
4.3. Непрерывные двумерные случайные величины
Определение.
Двумерная случайная величина
называется непрерывной,
если существует неотрицательная
интегрируемая в
функция
такая, что функция распределения
представима в виде:
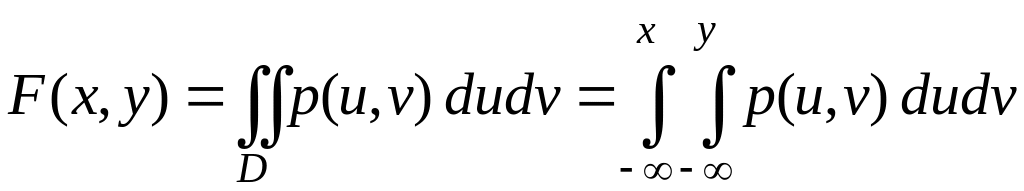(35)
(область интегрирования изображена на рис. 14).
EMBED Word.Picture.8
Рис. 14.
Функция называется плотностью распределения.
Замечание.
Для двойного интеграла
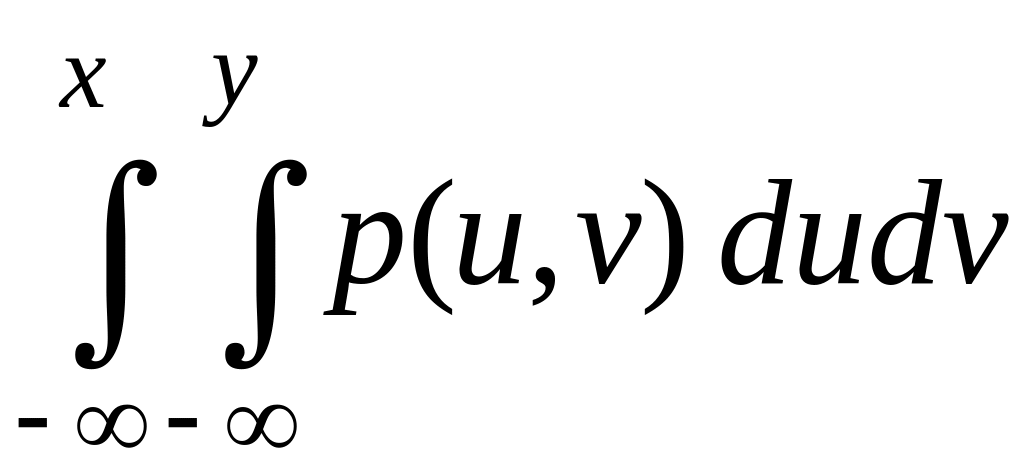с переменными верхними пределами
справедлива теорема, аналогичная теореме
о производной определенного интеграла
с переменным верхним пределом [12]:
.
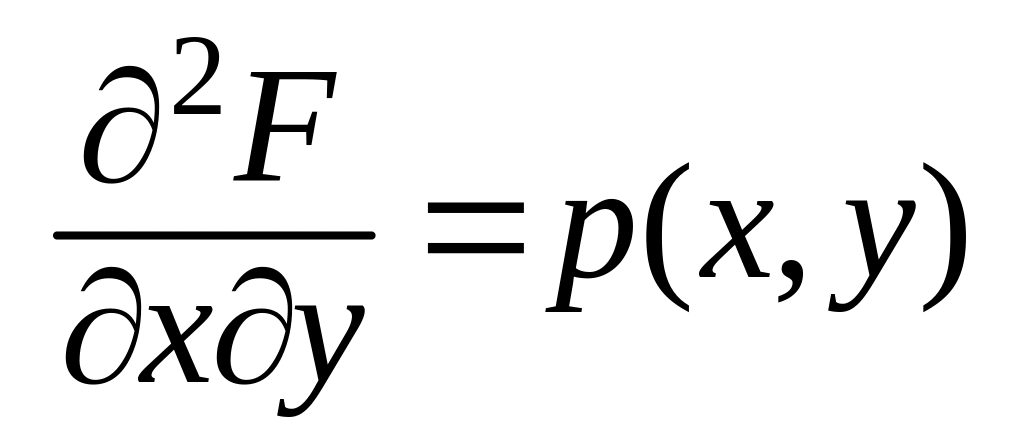Вероятностный смысл плотности
Пусть
двумерная случайная величина
непрерывна и имеет непрерывную плотность
.
Обозначим через
вероятность попадания случайной точки
в прямоугольник
с площадью
(рис. 15).
EMBED Word.Picture.8
Рис. 15.
По формулам (34) и (35):
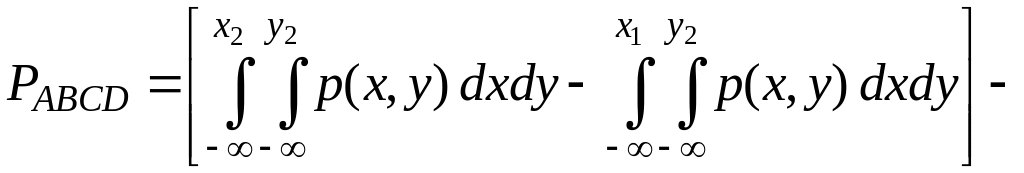
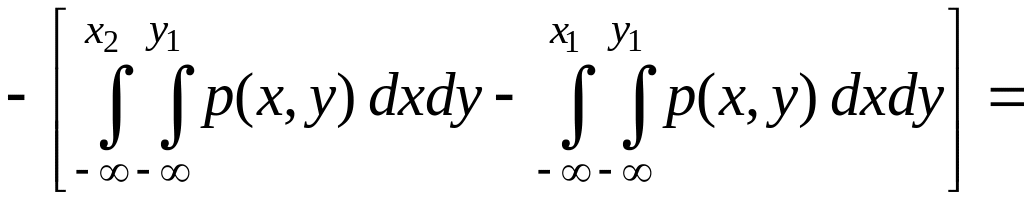
(применим свойство аддитивности к внешнему интегралу)
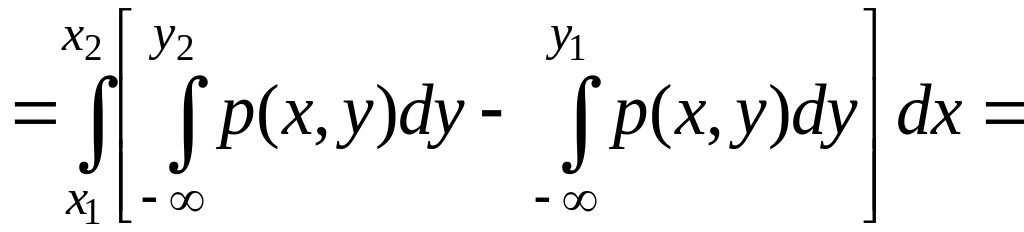
(применим свойство аддитивности к внутреннему интегралу)
.
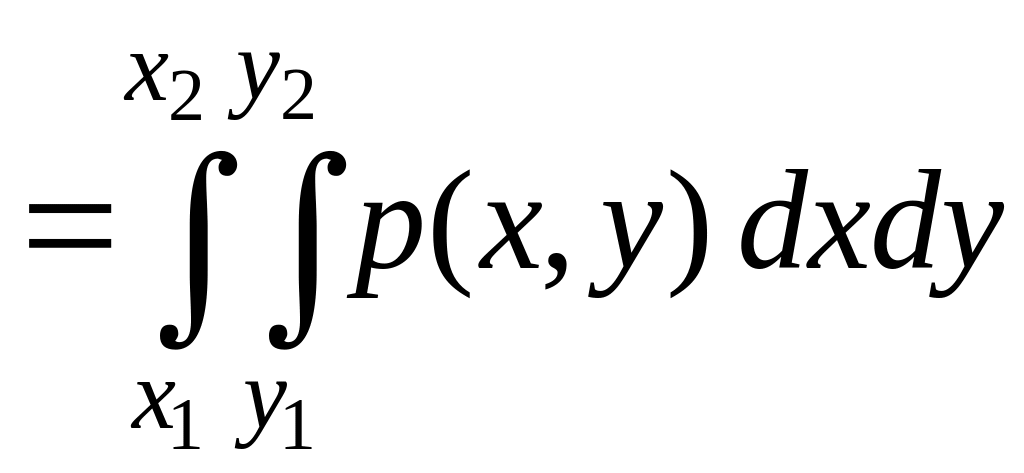Итак,
.
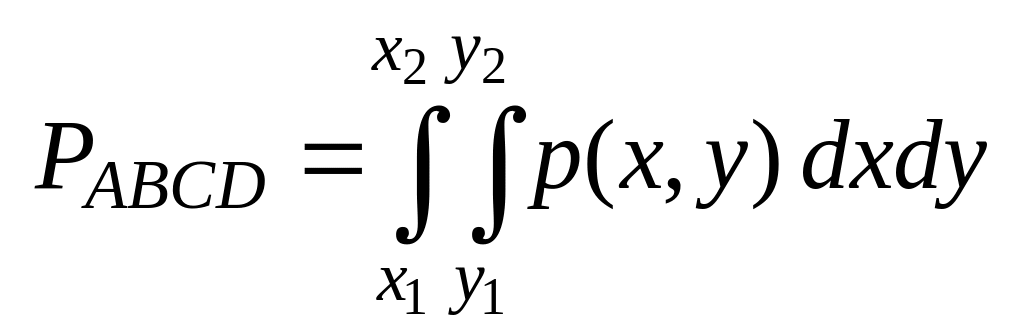(36)
Вывод: вероятность попадания непрерывно распределенной случайной точки в прямоугольник равна двойному интегралу от плотности по этому прямоугольнику.
Следствие:
Применяя к двойному интегралу в (36)
теорему о среднем, получаем для вероятности
попадания в прямоугольник ABCD
со сторонами
:
,
(37)
где
— некоторая точка прямоугольника.
Отсюда
.
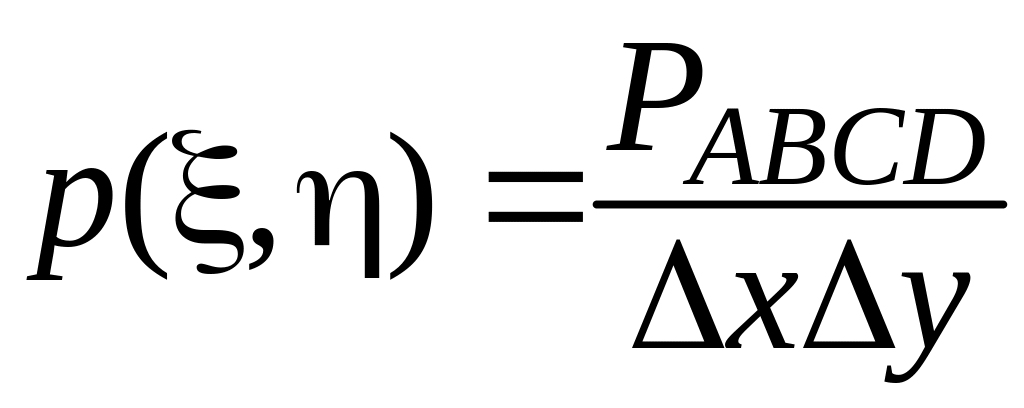Если теперь
,
то точка
неограниченно приближается к точке
,
так что
.
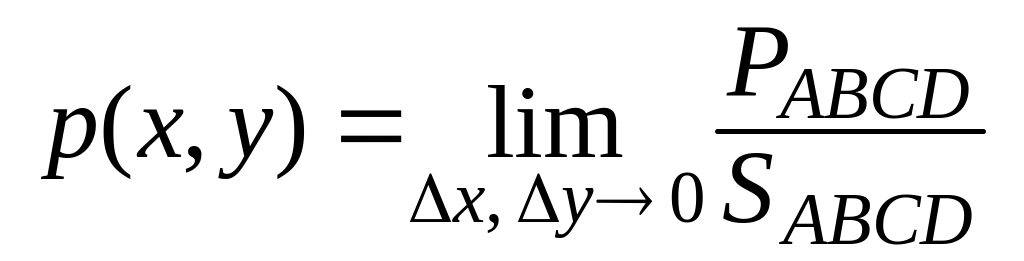(38)
Итак, плотность распределения непрерывной двумерной случайной величины при малых приближенно равна отношению вероятности попадания в малый прямоугольник к площади этого прямоугольника.