0

ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО

ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ВОДНЫХ КОММУНИКАЦИЙ»

————————————————————————————————

М.Ю. Ястребов

МАТЕМАТИКА

ТЕОРИЯ ВЕРОЯТНОСТЕЙ. ЧАСТЬ II.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Учебное пособие

Утверждено Редакционно-издательским советом

университета в качестве учебного пособия

Санкт-Петербург

2005

УДК

ББК

Рецензент:

Кандидат физико-математических наук, доцент

Кузнецов В.О.

Ястребов М.Ю. Математика. Теория вероятностей. Часть II. Случайные величины: Учебное пособие. — СПб: СПГУВК, 2005 — 66 С.

Учебное пособие предназначено для студентов второго курса экономических и технических специальностей. Оно соответствует рабочей программе дисциплины «Математика» и может быть использовано как при подготовке к экзамену, так и для текущих учебных занятий.

УДК

ББК

© Санкт-Петербургский государственный

Университет водных коммуникаций, 2005

Глава 1. Дискретные случайные Величины

1.1. Понятие случайной величины

Определение. Случайной величиной называется числовая величина, удовлетворяющая двум условиям:

1) в результате испытания она принимает неизвестные наперед значения;

2) принятие ею значения, лежащего в каком-либо наперед заданном промежутке, является случайным событием, имеющим определенную вероятность.

Замечание. Второе условие означает, что в теории вероятностей рассматриваются в качестве специальных объектов — случайных величин — не любые величины с неизвестными наперед значениями, а только такие, которые:

— во-первых, связаны с многократно воспроизводимыми (в неизменных контролируемых условиях) испытаниями;

— во-вторых, принимают значения из любого наперед

заданного диапазона с относительной частотой, которая проявляет при большом числе испытаний свойство устойчивости [13, п.2.4].

Будем обозначать случайные величины прописными латинскими буквами: и т. п.

1.2. Функция распределения случайной величины

Определение. Функцией распределения случайной величины называется функция , заданная при каждом формулой:

.

Таким образом, выражает вероятность случайного события, которое заключается в том, что в результате испытания случайная величина примет значение, меньшее аргумента .

Свойства функции распределения.

1. Значения функции распределения принадлежат отрезку : .

Действительно, есть вероятность некоторого случайного события, а вероятность всегда лежит в указанных пределах [13, п.3.2]. ▄

2. .

Доказательство. Введем случайные события:

, , ,

так что

.

Тогда , и правая часть есть сумма несовместных событий (рис. 1). Отсюда:

, и . ▄

3. Функция распределения является неубывающей:

при .

Доказательство. В предыдущих обозначениях событие влечет за

собой событие : . Следовательно, по свойству вероятности [13, п.3.2], выполняется неравенство , то есть . ▄

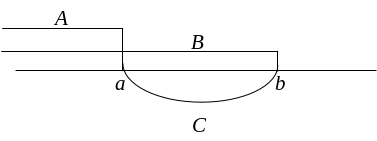
Рис.1.

4. Если все возможные значения случайной величины принадлежат отрезку , то:

при ;

при .

Доказательство. При событие является невозможным; поэтому . При событие является достоверным; поэтому

. ▄

Укажем без доказательства следующие свойства:

5. Поведение на бесконечности:

, или .

6. Функция распределения непрерывна слева, то есть для каждого левосторонний предел функции в точке равен значению функции в этой точке:

, или в другой записи: .

1.3. Закон распределения дискретной случайной величины

Определение. Случайная величина называется дискретной, если все ее возможные значения можно представить в виде конечной или бесконечной последовательности: .

Определение. Законом распределения дискретной случайной величины называется таблица (конечная или бесконечная), содержащая все ее возможные значения и вероятности принятия этих значений :

			…		…
			…		…

Будем обозначать закон распределения также в виде:

или .

Примеры. 1. Испытание: бросание игральной кости. Случайная величина — количество выпавших очков. Возможные значения — числа . Для каждого из этих значений схема равновозможных исходов дает вероятность 1/6. Закон распределения имеет вид:

	1	2	3	4	5	6
	1/6	1/6	1/6	1/6	1/6	1/6

2. Испытание: три раза бросается монета. Случайная величина — количество выпадений герба. Возможные значения – числа . Вероятности значений находятся по схеме Бернулли как вероятности числа успехов (см. [13], п. 3.11), где вероятность успеха в отдельном испытании , вероятность неудачи :

;

;

;

.

Закон распределения имеет вид:

	0	1	2	3
	1/8	3/8	3/8	1/8

3. Испытание: Стрельба по мишени до первого попадания. Вероятность попадания при отдельном выстреле равна . Случайная величина — количество произведенных выстрелов. Возможные значения: ; множество значений бесконечно. Найдем вероятности этих значений, считая результаты отдельных выстрелов независимыми событиями.

Если первое попадание произошло при -м выстреле, то первые выстрелов были промахами, а последний, -й, — попаданием. Введем события — попадание при -м выстреле ( ), так что

.

Тогда по теореме умножения для независимых событий (см. [13], п. 3.8):

.

Теорема. Сумма вероятностей закона распределения дискретной случайной величины равна :

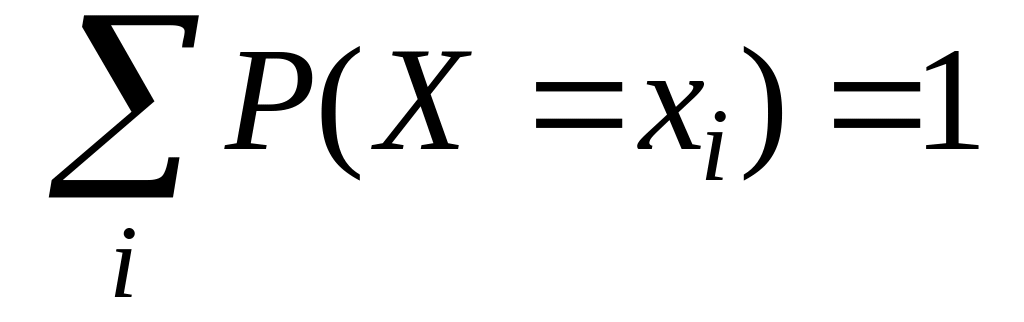. (1)

(если множество возможных значений бесконечна, то сумма в (1) понимается как сумма ряда, то есть как предел частичных сумм).

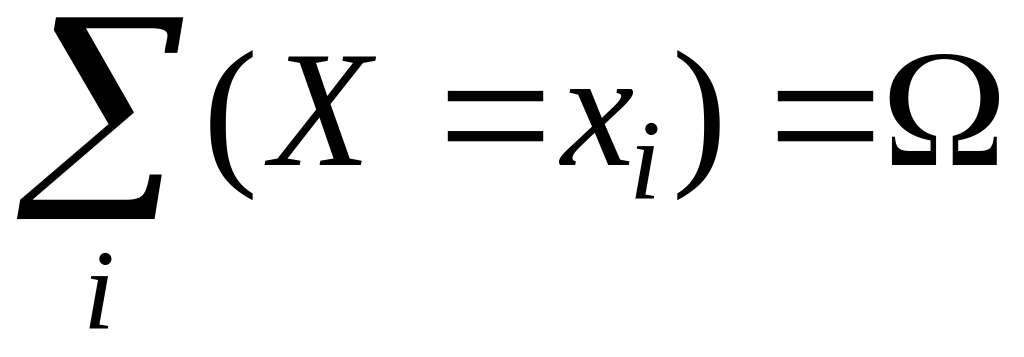Доказательство. События при разных попарно несовместны. Поскольку одно из возможных значений обязательно реализуется в результате испытания, то . Тогда

. ▄
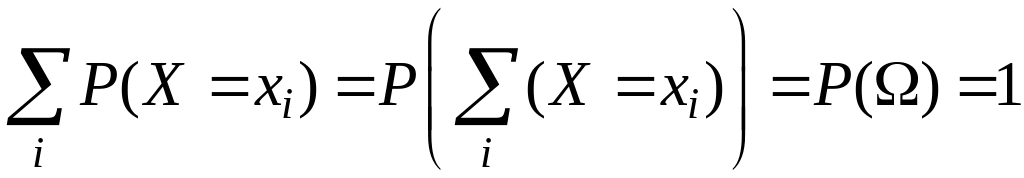