10. Параметрическое задание функции

Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр.

Инвариантность формы дифференциала

Формула дифференциала функции имеет вид

где - дифференциал независимой переменной.

Пусть теперь дана сложная (дифференцируемая) функция , где , .

Тогда по формуле производной сложной функции находим

,

так как .

Итак, , т.е. формула дифференциала имеет один и тот же вид для независимой переменной и для промежуточного аргумента , представляющего собой дифференцируемую функцию от .

Это свойство принято называть свойством инвариантности формулы или формы дифференциала. Заметим, что производная этим свойством не обладает.

11. Дифференцирование параметрически заданных функций.

Если функция задана в явном виде y=f(x), то всегда можно записать её в неявном виде y-f(x)=0, а также в параметрической форме

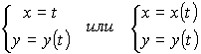
От вида F(x,y)=0 не всегда возможно перейти к виду y=f(x) или x=φ (y), так как уравнение F(x,y)=0 может оказаться неразреш имым относительно y или x . Лего перейти от параметрического представления функции к уравнению вида y=f(x). Для этого из первого уравнения x=x(t) нужно найти t=t(x), если конечно это возможно , и подставить его во второе уравнение y=y(t)

y=y[t(x)]=f(x)

От параметрического представления функции к уравнению вида F(x,y)=0 можно прийти путем исключения параметра t, если это возможно. Уравнения y=f(x) и F(x, y)=0 служат различными аналитическими представлениями одной и той же функции F[x, f(x)]=0. Параметрические уравнения

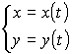
и уравнение F(x, y)=0 представляют одну и ту же функцию, если F(x(t), y(t))=0. Наконец, параметрические уравнения определяют ту же функцию, что и уравнение y=f(x), если

y(t)=f [ x(t) ].

Найдем производную функции y по x в случае, когда она задана в параметрическом виде. Для этого будем рассматривать t как функцию от x. То есть t=t(x). Тогда y=y[t(x)]. Продифференцируем y как сложную функцию от x, т.е. по формуле

и применим формулу, связывающую производные обратных функций:

Введя обозначения

,      

получим

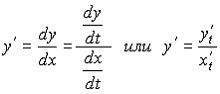
Пример.

Теперь найдем вторую производную от функции, заданной в параметрической форме.    Из предидущего уравнения и определения второй производной следует, что

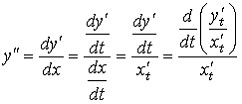
но

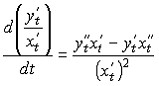
Следовательно

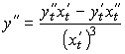
где

           

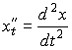
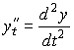
12. Производные и дифференциалы высших порядков и их свойства. Формулы Лейбница для производной произведения

Определение 5. Пусть функция f(x) определена на промежутке и в каждой точке промежутка имеет производную f'(x), тогда производная функции f'(x), если она существует, называется второй производной функции f(x). Обозначение: f"(x); f⁽²⁾(x). Аналогично, вводятся производные f⁽ⁿ⁾(x) любого порядка. Определение 6. Дифференциал от первого дифференциала в недляорой точке а называется вторым дифференциалом функции в этой точке. Обозначение: d²y(a); d²f(a); d²y; d²f. Аналогично, вводятся дифференциалы любого порядка: dⁿy = d(d^n-1y). Если х - независимая переменная, то d²y(a) = f"(a) • dx²; d²y(a) = f²(a) • dxⁿ, n N Производные высших порядков недляорых элементарных функций

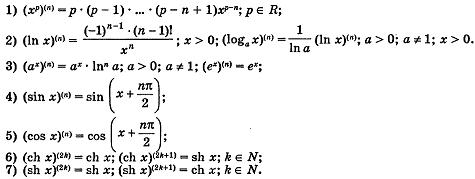
Свойства производных и дифференциалов высших порядков

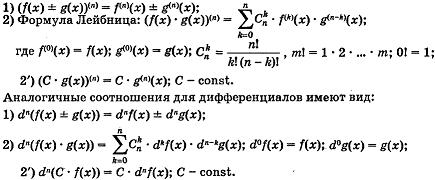
Определение 5. Пусть функция f(x) определена на промежутке и в каждой точке промежутка имеет производную f'(x), тогда производная функции f'(x), если она существует, называется второй производной функции f(x). Обозначение: f"(x); f⁽²⁾(x). Аналогично, вводятся производные f⁽ⁿ⁾(x) любого порядка. Определение 6. Дифференциал от первого дифференциала в недляорой точке а называется вторым дифференциалом функции в этой точке. Обозначение: d²y(a); d²f(a); d²y; d²f. Аналогично, вводятся дифференциалы любого порядка: dⁿy = d(d^n-1y). Если х - независимая переменная, то d²y(a) = f"(a) • dx²; d²y(a) = f²(a) • dxⁿ, n N Производные высших порядков недляорых элементарных функций

Свойства производных и дифференциалов высших порядков