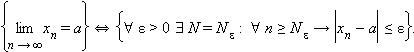Свойства функции  1)  2)    не является ни четной, ни нечетной; 3)    возрастает на  4)    не ограничена сверху, ограничена снизу; 5)    не имеет наибольшего значения;  6)    непрерывна; 7)  8)    выпукла вниз. Рассмотрим степенную функцию   для случая, когда   правильная дробь  Все рассмотренное в § 40 в отношении функции   или, что то же самое,   (ее график изображен на рис. 169) имеет место и по отношению к любой степенной функции вида   правильная дробь (числитель меньше знаменателя). График функции у = х^г изображен на рис. 187.

Свойства функции  1)  2)    не является ни четной, ни нечетной; 3)    возрастает на  4)    не ограничена сверху, ограничена снизу; 5)    не имеет наибольшего значения;  6)    непрерывна; 7)  8)    выпукла вверх. Нам осталось рассмотреть степенную функцию вида   Область ее определения — открытый луч (0, + оо). Выше мы построили график степенной функции у = х^-n, где п — натуральное число. При х > 0 график функции у =х^-п пoхож на ветвь гиперболы (рис. 184). Точно так же обстоит дело для любой степенной функции вида  , график которой изображен на рис. 188. Отметим, что график данной функции имеет горизонтальную асимптоту у = 0 и вертикальную асимптоту х = 0.

Свойства функции  1)  2)    не является ни четной, ни нечетной; 3)    убывает на (0, + оо); 4)    не ограничена сверху, ограничена снизу; 5)    не имеет ни наибольшего, ни наименьшего значения; 6)    непрерывна; 7)  8)    выпукла вниз. Вы заметили, наверное, что мы пока ничего не сказали о свойстве дифференцируемости степенной функции. Начнем издалека. Мы знаем, чему равна производная функции у =хⁿ, где п — натуральное число:

Нетрудно найти производную степенной функции у = х^-n, где n — натуральное число. Для этого надо переписать выражение х^-n в виде   и воспользоваться правилом дифференцирования дроби:

Итак, для любого   справедлива формула

Формулы (1) и (2) можно объединить в одну:

где m — любое целое число. Идем дальше. Мы знаем, что    Эту формулу можно записать следующим образом:

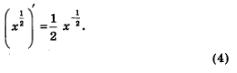И формула (3), и формула (4) являются частными случаями общего утверждения (которое мы приводим без доказательства).

Например,

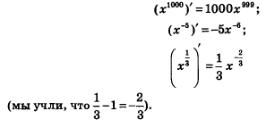Нетрудно получить и соответствующую формулу для интегрирования степенной функции: если

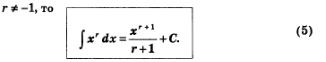
В самом деле,  Значит, функция   является первообразной для функции у = х^г, а потому справедлива формула (5). Например,

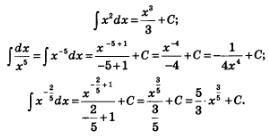Рассмотрим ряд примеров.

Множество - это совокупность объектов, рассматриваемая как одно целое. Понятие множества принимается за основное, т. е. не сводимое к другим понятиям. Объекты, составляющие данное множество, называются его элементами. Основное отношение между элементом a и содержащим его множеством A обозначается так  (a есть элемент множества A; или a принадлежит A, или Aсодержит a). Если a не является элементом множества A, то пишут  (a не входит в A, A не содержит a). 

 Если каждый элемент множества A входит в B, но множество B содержит хотя бы один элемент, не входящий в A, т. е. если   и , то A называется собственным подмножеством B, а B - собственным надмножеством A. В этом случае пишут  . Например, запись   и   означают одно и то же, а именно, что множество A не пусто.

Число — абстракция, используемая для количественной характеристики объектов. Числа возникли еще в первобытном обществе в связи с потребностью людей считать предметы. С течением времени по мере развития науки число превратилось в важнейшее математическое понятие.

Для решения задач и доказательства различных теорем необходимо понимать, какие бывают виды чисел. Основные виды чисел включают в себя: натуральные числа, целые числа, рациональные числа, действительные числа.

Натуральные числа – это числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий»...). Множество натуральных чисел обозначается латинской буквой N (можно запомнить, опираясь на английское слово natural). Можно сказать, что N ={1,2,3,....}

Целые числа – это числа из множества {0, 1, -1, 2, -2, ....}. Это множество состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0 (нуль). Целые числа обозначаются латинской буквой Z. Можно сказать, чтоZ={1,2,3,....}.

Рациональные числа – это числа, представимые в виде дроби , где m — целое число, а n — натуральное число. Для обозначения рациональных чисел используется латинская буква Q. Все натуральные и целые числа – рациональные. Также в качестве примеров рациональных чисел можно привести:  , , .

Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой  R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными. Примеры иррациональных чисел – это , , .

Любое действительное число можно отобразить на числовой прямой:

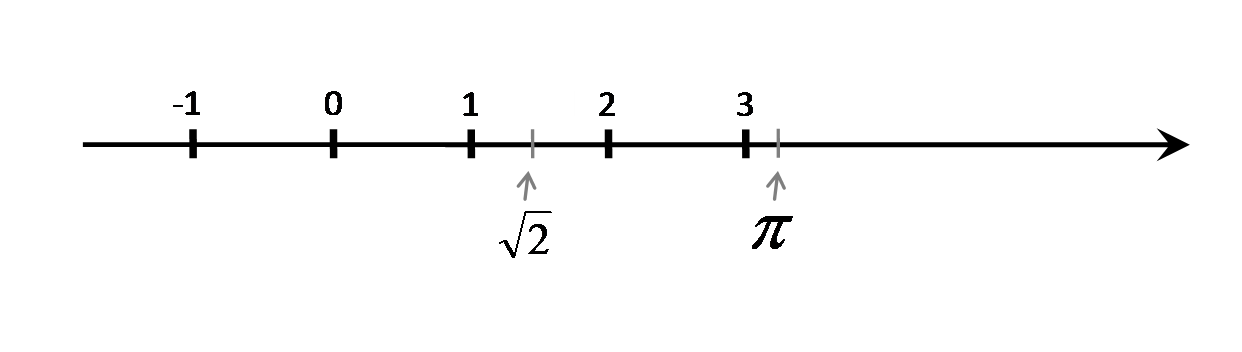
Для перечисленных выше множеств чисел справедливо следующее высказывание:

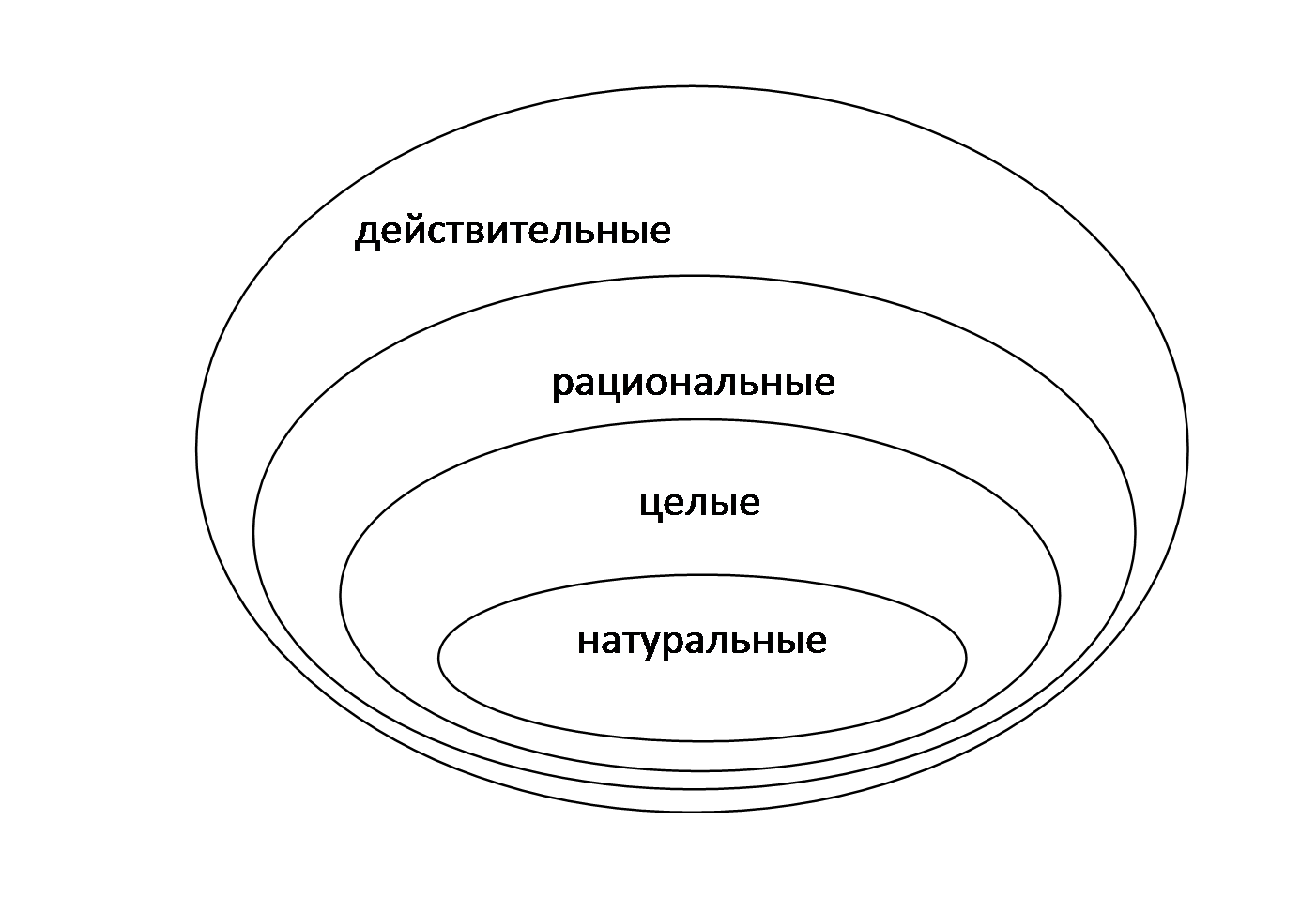
То есть множество натуральных чисел входит во множество целых чисел. Множество целых чисел входит во множество рациональных чисел. А множество рациональных чисел входит во множество действительных чисел. Это высказывание можно проиллюстрировать с помощью кругов Эйлера.

Среднее гармоническое – обратное среднему арифметическому.

Среднее геометрическое.

a_{ср.геом=} ⁿ

a1 · a2 · … · an

Предельная точка числового множества

В частности, предельной точкой числового множества, имеющего бесконечное число элементов, называется точка числовой прямой, в любой окрестности которой содержится бесконечно много элементов этого множества. Также можно считать предельной точкой такого множества  , если из некоторых его элементов можно составить бесконечно большую последовательность с попарно различными отрицательными элементами. Если же можно составить бесконечно большую последовательность с попарно различными положительными элементами, то можно считать предельной точкой  .

Верхняя предельная точка числового множества — это наибольшая из его предельных точек.

Нижняя предельная точка числового множества — это наименьшая из его предельных точек.

Свойства

• У любого ограниченного числового множества, имеющего бесконечное число элементов, существуют и верхняя, и нижняя предельные точки (в множестве вещественных чисел). Если добавить в множество вещественных чисел   и  , то в получившемся множестве предельные точки имеют вообще все числовые множества с бесконечным числом элементов.

• Из элементов любого ограниченного числового множества, имеющего бесконечное число элементов, можно выделить сходящуюся последовательность, элементы которой попарно различны.

Предельная точка последовательности

Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности.

 — предельная точка последовательности 

Наибольшая предельная точка последовательности называется её верхним пределом, а наименьшая предельная точка — нижним пределом.

Иногда в множество возможных предельных точек включают « » и « ». Так если из последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой отрицательны, то говорят, что « » является предельной точкой этой последовательности. Если же из последовательности можно выделить бесконечно большую подпоследовательность с исключительно положительными элементами, то говорят, что « » является её предельной точкой.^[1] При этом, разумеется, у последовательности могут быть и другие предельные точки.

Свойства

• Точка является предельной точкой последовательности тогда и только тогда, когда из этой последовательности можно выделить подпоследовательность, сходящуюся к этой точке.

 — предельная точка последовательности 

Иногда это свойство принимают за определение, а приведённое выше определение — за свойство.

• Всякая сходящаяся числовая последовательность имеет только одну предельную точку.

 — предельные точки последовательности 

• Предельная точка любой сходящейся числовой последовательности совпадает с её пределом.

 — предельная точка последовательности 

• Для любого конечного или счётного множества точек можно построить последовательность, для которой эти точки будут являться предельными и никакие, кроме них.

• У произвольной числовой последовальности имеется хотя бы одна предельная точка (либо вещественная, либо бесконечность).

Примеры

• У последовательности из единиц   существует единственная предельная точка 1.

• У последовательности   существует единственная предельная точка 0.

• У последовательности натуральных чисел 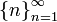  нет предельных точек (или, в других терминах, имеется предельная точка  ).

• У последовательности 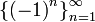  существуют две предельные точки: -1 и +1.

• У последовательности из всех рациональных чисел  , занумерованных произвольным образом, существует бесконечно много предельных точек.

Предел последовательности

Если каждому натуральному числу n поставлено в соответствие некоторое вещественное число    то говорят, что задана числовая последовательность   Кратко она обозначается символом      называют n-м членом последовательности. Совокупность этих чисел называют множеством значений последовательности.

Существует несколько способов задания числовых последовательностей.

1. Последовательность может быть задана при помощи формулы, позволяющей вычислить каждый ее член по номеру (например,   ).

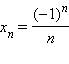2. Часто последовательность задается при помощи рекуррентной формулы, позволяющей определить каждый член последовательности по одному или нескольким предыдущим; при этом необходимо задание одного или нескольких первых членов последовательности. К таковым относятся арифметическая игеометрическая прогрессии или, например, последовательность Фибоначчи, задаваемая формулой 

   xn + 2 = xn + 1 + xn при n > 0

3. и условиями x₁ = 1, x₂ = 1.

4. Иногда последовательность задается описанием ее членов, например, последовательность, у которой x_n равен n-му знаку после запятой в десятичной записи числа π = 3,14159265358979323..., задается следующим образом: x₁ = 1, x₂ = 4, x₃ = 1, x₄ = 5, x₅ = 9, x₆ = 2, x₇ = 6, x₈ = 5, x₉ = 3, x₁₀ = 5 и т. д.

Число a называется пределом последовательности {x_n}, если для каждого ε > 0 существует такой номер N_ε, что для всех n ≥ N_ε выполняется неравенство 

|xn – a| < ε,

т. е.   При этом пишут, что 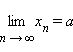  или   при n → ∞. Кратко это определение можно записать так: 

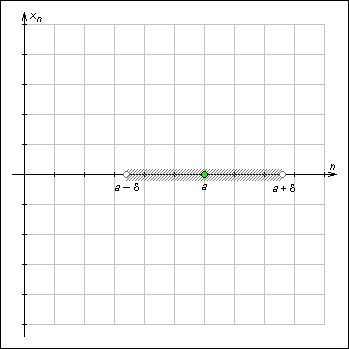
Интервал (a – ε; a + ε) называют ε-окрестностью точки a.

Рисунок 1.1.1.1. ε-окрестность точки a.

Проще говоря, число a называется пределом последовательности {x_n}, если в любой ε-окрестности точки aлежат все члены последовательности {x_n}, за исключением, может быть, конечного их числа. Отсюда легко заметить, что изменение конечного числа членов последовательности не влияет ни на факт существования предела, ни на величину последнего.

Так, если 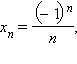  то   Действительно, выбрав для произвольного ε > 0   получаем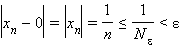  , так как 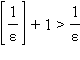  . Здесь существенно, что N_ε зависит от ε.

Для стабилизирующейся последовательности (т. е. последовательности {x_n} такой, что x_n = a при n ≥ n₀) в качестве N_ε для любого ε можно взять n₀.

Последовательность, у которой существует предел, называется сходящейся. Если никакое число не является пределом последовательности, то она называется расходящейся.

Можно показать, что числовая последовательность имеет только один предел.

Последовательность   называется возрастающей, если для любого   выполняется неравенство 

xn + 1 > xn.

Последовательность   называется убывающей, если для любого   выполняется неравенство 

xn + 1 < xn.

Если в этих определениях неравенство будет нестрогим, то последовательности будут называться соответственно неубывающей и невозрастающей.

Возрастающие и убывающие последовательности называют строго монотонными. Неубывающие и невозрастающие последовательности называютмонотонными.

При a > 0, a \ne 1, определена функция y = a ^x , отличная от постоянной. Эта функция называется показательной функцией с основанием a. 

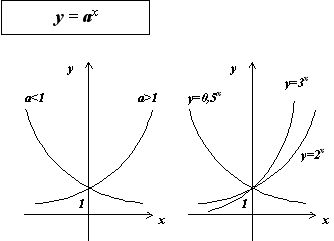
Основные свойства показательной функции y = a ^x при a > 1:

• Область определения функции - вся числовая прямая.

• Область значений функции - промежуток (0;+ ∞).

• Функция строго монотонно возрастает на всей числовой прямой, то есть, если x₁< x_{2 ,} то a^x₁ < a^x₂ .

• При x = 0 значение функции равно 1.

• Если x > 0 , то a ^x > 1 и если x < 0, то 0 < a < 1.

Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на рисунке.

Основные свойства показательной функции y = a ^x при 0 < a < 1:

• Область определения функции - вся числовая прямая.

• Область значений функции - промежуток (0;+∞).

• Функция строго монотонно возрастает на всей числовой прямой, то есть, если x₁< x_{2 ,} то a^x₁ > a^x₂ .

• При x = 0 значение функции равно 1.

• Если x > 0 , то 0 < a < 1 и если x < 0, то a ^x > 1.

Функция и её свойства

Функция- зависимость переменной у от переменной x, если

каждому значению х соответствует единственное значение у.

Переменная х- независимая переменная или аргумент.

Переменная у- зависимая переменная

Значение функции- значение у, соответствующее заданному значению х.

Область определения функции- все значения, которые принимает независимая

переменная.

Область значений функции (множество значений)- все значения, которые

принимает функция.

Функция является четной- если для любого х из области определения

функции выполняется равенство f(x)=f(-x)

Функция является нечетной- если для любого х из области

определения функции выполняется равенство f(-x)=-f(x)

Возрастающая функция- если для любых х₁ и х₂

, таких, что х₁< х₂, выполняется

неравенство f(х₁)<f(х₂)

Убывающая функция- если для любых х₁ и х₂

, таких, что х₁< х₂, выполняется

неравенство f(х₁)>f(х₂)

Способы задания функции

¨ Чтобы задать функцию, нужно указать способ, с помощью которого для

каждого значения аргумента можно найти соответствующее значение функции.

Наиболее употребительным является способ задания функции с помощью формулы

у=f(x), где f(x)-

некоторое

выражение с переменной х

. В таком случае говорят, что функция задана формулой или что функция задана

аналитически.

¨ На практике часто используется табличный способ задания

функции. При этом способе приводится таблица, указывающая значения функции для

имеющихся в таблице значений аргумента. Примерами табличного задания функции

являются таблица квадратов, таблица кубов.

Виды функций и их свойства

1) Постоянная функция- функция, заданная формулой у=b, где

b-некоторое число. Графиком постоянной функции у=b является прямая,

параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат

2) Прямая пропорциональность- функция, заданная формулой у=kx,

где к¹0. Число k называется коэффициентом пропорциональности

.

Cвойства функции y=kx:

1. Область определения функции- множество всех действительных чисел

2. y=kx - нечетная функция

3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой

3)Линейная функция- функция, которая задана формулой y=kx+b, где

k и b-действительные числа. Если в частности, k=0, то

получаем постоянную функцию y=b; если b=0, то получаем прямую

пропорциональность y=kx.

Свойства функции y=kx+b:

1. Область определения- множество всех действительных чисел

2. Функция y=kx+b общего вида, т.е. ни чётна, ни нечётна.

3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой

Графиком функции является прямая.

4)Обратная пропорциональность- функция, заданная формулой y=k/х,

где k¹0 Число k называют коэффициентом обратной

пропорциональности.

Свойства функции y=k/x:

1. Область определения- множество всех действительных чисел кроме нуля

2. y=k/x- нечетная функция

3. Если k>0, то функция убывает на промежутке (0;+¥) и на промежутке

(-¥;0). Если k<0, то функция возрастает на промежутке (-¥;0) и на

промежутке (0;+¥).

Графиком функции является гипербола.

5)Функция y=x²

Свойства функции y=x²:

1. Область определения- вся числовая прямая

2. y=x² - четная функция

3. На промежутке [0;+¥) функция возрастает

4. На промежутке (-¥;0] функция убывает

Графиком функции является парабола.

6)Функция y=x³

Свойства функции y=x³:

1. Область определения- вся числовая прямая

2. y=x³ -нечетная функция

3. Функция возрастает на всей числовой прямой

Графиком функции является кубическая парабола

7)Степенная функция с натуральным показателем- функция, заданная формулой

y=xⁿ, где n- натуральное число. При n=1 получаем функцию

y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x²;

y=x³. Их свойства рассмотрены выше.

Пусть n- произвольное четное число, большее двух: 4,6,8... В этом случае функция

y=xⁿ обладает теми же свойствами, что и функция y=x².

График функции напоминает параболу y=x², только ветви графика при

|х|>1 тем круче идут вверх, чем больше n, а при |х|<1 тем «теснее

прижимаются» к оси Х, чем больше n.

Пусть n- произвольное нечетное число, большее трех: 5,7,9... В этом случае

функция y=xⁿ обладает теми же свойствами, что и функция y=x

³. График функции напоминает кубическую параболу.

8)Степенная функция с целым отрицательным показателем- функция, заданная

формулой y=x^-n, где n- натуральное число. При n=1

получаем y=1/х, свойства этой функции рассмотрены в п.4.

Пусть n- нечетное число, большее единицы: 3,5,7... В этом случае функция y=x

^-n обладает в основном теми же свойствами, что и функция y=1/х.

Пусть n- четное число, например n=2.

Свойства функции y=x^-2:

1. Функция определена при всех x¹0

2. y=x^-2 - четная функция

3. Функция убывает на (0;+¥) и возрастает на (-¥;0).

Теми же свойствами обладают любые функции при четном n, большем двух.

9)Функция y=Öх

Свойства функции y=Öх:

1. Область определения - луч [0;+¥).

2. Функция y=Öх - общего вида

3. Функция возрастает на луче [0;+¥).

10)Функция y=³Öх

Свойства функции y=³Öх:

1. Область определения- вся числовая прямая

2. Функция y=³Öх нечетна.

3. Функция возрастает на всей числовой прямой.

11)Функция y=ⁿÖх

При четном n функция обладает теми же свойствами, что и функция y=Öх

. При нечетном n функция y=ⁿÖх обладает теми же

свойствами, что и функция y=³Öх.

12)Степенная функция с положительным дробным показателем- функция,

заданная формулой y=x^r, где r- положительная

несократимая дробь.

Свойства функции y=x^r:

1. Область определения- луч [0;+¥).

2. Функция общего вида

3. Функция возрастает на [0;+¥).

На рисунке изображен график функции y=x^5/2. Он заключен

между графиками функций y=x² и y=x³, заданных на

промежутке [0;+¥).Подобный вид имеет любой график функции вида y=x

^r, где r>1.

На рисунке изображен график функции y=x^2/3. Подобный вид

имеет график любой степенной функции y=x^r , где 0<r<1

13)Степенная функция с отрицательным дробным показателем-функция,

заданная формулой y=x^-r, где r- положительная

несократимая дробь.

Свойства функции y=x^-r:

1. Обл. определения -промежуток (0;+¥)

2. Функция общего вида

3. Функция убывает на (0;+¥)

14)Обратная функция

Если функция y=f(x) такова, что для любого ее значения y_o

уравнение f(x)=y_o имеет относительно х единственный

корень, то говорят, что функция f обратима.

Если функция y=f(x) определена и возрастает (убывает) на промежутке Х и

областью ее значений является промежуток Y, то у нее существует обратная

функция, причем обратная функция определена и возрастает(убывает) на Y.

Таким образом, чтобы построить график функции, обратной к функции y=f(x),

надо график функции y=f(x) подвергнуть преобразованию симметрии относительно

прямой y=x.

15)Сложная функция- функция, аргументом которой является другая любая функция.

Возьмем, к примеру, функцию y=x+4. Подставим в аргумент функцию y=x+2.

Получается: y(x+2)=x+2+4=x+6. Это и будет являться сложной функцией.