3. Основные объекты, изучаемые в сопротивлении материалов: брус (стержень), пласти­на, оболочка, массивное тело. Понятие о расчетной схеме конструкции.

Под стержнем понимается тело, длина которого много больше его поперечных размеров. Осевая линия стержня является геометрическим местом центров тяжести поперечных сечений. Стержень, работающий на изгиб, часто называют брусом или балкой. С точки зрения сопротивления материалов балкой являет­ся не только строительная балка, но и вал, болт, ось железнодорож­ного вагона, зуб шестерни и т. д. В сопротивлении материалов рас­сматриваются только стержневые системы.

Расчетная схема - упрощенное изображение элемента или всей конструкции, учитывающее только основные факторы, опреде­ляющие их поведение под нагрузкой.

При составлении расчетной схемы сооружения используются сле­дующие принципы:

•стержни заменяются осевыми линиями;

•нагрузки с поверхности стержней переносятся на оси, при этом силовая плоскость будет совпадать с плоскостью рисунка;

• реальные опорные устройства и связи между элементами заме­няются идеальными связями (шарнирами, стержнями);

• поперечные сечения стержней независимо от их формы характе­ризуются численными значениями площадей и моментов инер­ции.

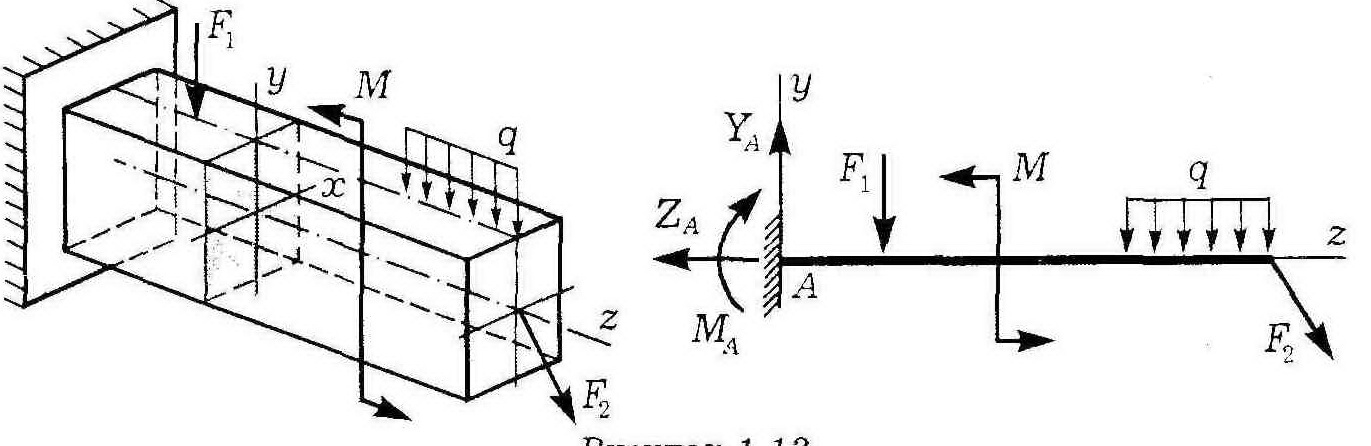
4. Главный вектор и главный момент внутренних сил в сечении. Внутренние силы в по­перечном сечении бруса.

Под воздействием нагрузки твердое те­ло деформируется. В нем возникают внут­ренние усилия, уравновешивающие на­грузку и препятствующие разрушению тел. Они воздействуют на каждую частицу тела. Если мысленно рассечь тело произвольной плоскостью и отбросить одну из частей, то действующие в оставшемся сечении внутренние усилия можно просуммировать и привести к его центру тяжести.

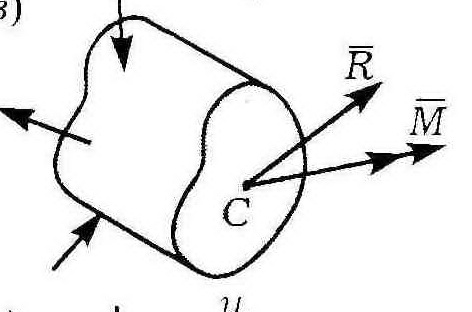
Полученный главный вектор R и главный момент M внутренних усилий в поперечных сечениях стержней расклады­ваются в декартовой системе координат следующим образом:

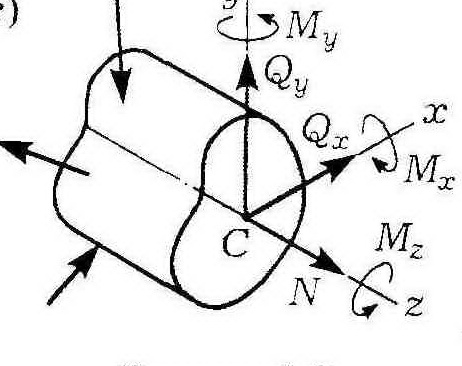
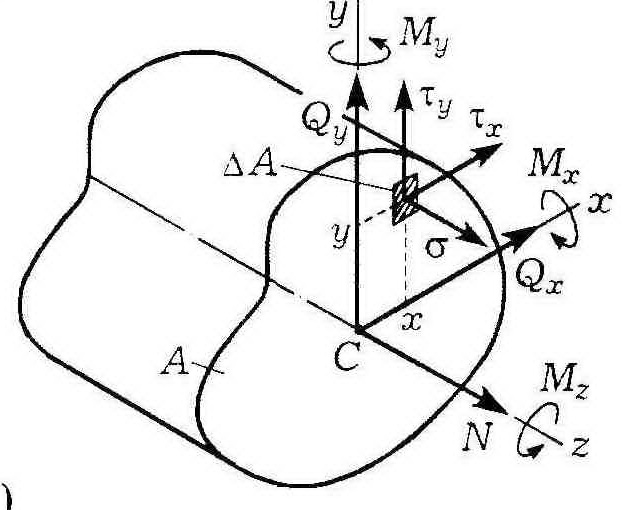
Здесь ось z перпендикулярна плоскости поперечного сечения стержня, т.е. совпадает с его осью; оси х, у лежат в плоскости по­перечного сечения. Компоненты (факторы) внутренних усилий носят следующие названия: N - продольная сила; Q_X,Q_Y - поперечные силы; Мк - крутящий момент; Мx, Му - изгибающие моменты. В зависимо­сти от наличия тех или иных внутренних факторов в поперечных сече­ниях судят о виде деформации стержня.

В зависимости от наличия тех или иных внутренних факторов в поперечных сечениях судят о виде деформации.

Возможны следующие простые виды деформирования стержней:

• только N_≠ О - центральное растяже­ние (сжатие);

•только M_Z ≠ 0 - кручение;

• только M_X ≠ 0 (или M_Y ≠ 0 ) – прямой чистый изгиб;

• только M_X≠ 0 и Q_Y ≠ 0(или M_Y≠ 0 и Q_X≠0 ) - поперечный изгиб.

Выделяют также сложные виды де­формирования стержней:

• только M_X≠ 0 и M_Y≠0 - косой изгиб;

• N ≠ 0, M_X≠ 0 , M_Y≠ 0 (один из Мх, Му может отсутствовать) - изгиб с растя­жением (сжатием);

• Мх ≠ 0, Му ≠ 0 , Мz ≠ О (один из Мх, Му может отсутствовать) -изгиб с кручением.

5. Напряжения. Их связь с внутренними силовыми факторами.

Выделим вокруг произвольной точки сечения А площадку ΔА, а равнодействующую внут­ренних сил на этой площадке обозначим ΔК.

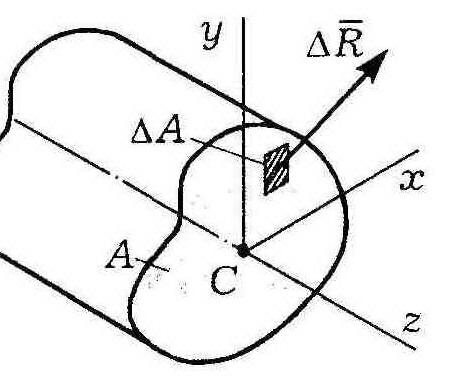
Отношение

п редставляет собой среднее напряжение на указанной площадке. При уменьше­нии размеров площадки (стягивании ее в данную точку) в пределе получается на­пряжение в точке рассматриваемого се­чения

Вектор р называют полным на­пряжением в рассматриваемой точке сечения.

Вектор напряже­ния p можно разложить по осям координат на нормальное напряжение σ , перпендикулярное к сечению, и два ка­сательных напряжения , лежащих в плоскости сечения.

Нормаль­ные и касательные напряжения влияют на прочность материала по-разному. Нормальные напряжения препятствуют отрыву одной части элемента от другой или их взаимному прижатию. Касательные на­пряжения препятствуют взаимному сдвигу.

Совокупность всех напряжений, действующих по различным площадкам, проходящим через рассматриваемую точку, представля­ет собой напряженное состояние в этой точке.

с вязь с внутренними силовыми факторами . Внутренние силы и моменты являются статическим эквивален­том напряжений, действующих по всему сечению. Следовательно, их связь можно получить, суммируя по всей площади сечения элементарные силы (σdA,τ_xdA,τ_ydA ) или беря момент этих сил относительно осей координат:

Полученные выражения для практических расчетов непо­средственно использовать нельзя, так как закон распределения на­пряжений по сечению неизвестен. Если же, пользуясь теми или ины­ми соображениями, удается установить закон распределения σ и τ по сечению, то по формулам можно найти и сами напряжения.