49. Определение перемещений методом интеграла Мора.

49. Правило Верещагина.

51. Формула Cимпсона, Мюллера-Бреслау.

Формула Симпсона: в общем случае сложных эпюр для вычисления интеграла Мора удобно использовать формулу Симпсона – одну из самых распространенных квадратных формул. Интеграл от функции f(z) можно приближенно вычислить по Симпсону следующим образом:

Эта формула основана на аппроксимировании – замене подынтегральной функции квадратной параболой, проходящей через крайние и среднюю ординаты f(a), f(b), f(c). Формула Симпсона для вычисления интеграла Мора га участках постоянной жесткости является точной, если обе функции f1(z), f2(z) линейные или одна из них линейная, а вторая квадратичная.

52. Основы метода сил.

Этот метод широко используется для расчета статически неопределенных стержневых систем. Последовательность расчета неопределенной системы по методу сил следующие:

1. определяется степень статической неопределенности путем подсчета лишних связей.

2. выбирается основная система метода сил, которая получается из заданной системы после удаления лишних связей. Удаленные связи заменяются лишними неизвестными усилиями, возникающими в этих связях.

3. составляются уравнения перемещений, которые выражают условия совместимости перемещений основной системы с заданной, статически неопределенной системой. Если перемещение в основной системе по направлению отброшенных связей в основной системе должны быть = 0, то уравнения перемещений выражают равенство нулю этих перемещений.

4. полученная система канонических уравнений является системой линейных алгебраических неоднородных уравнений и она решается каким – либо методом (например: метод Гаусса).

5. после определения значений лишних неизвестных усилий, определяют внутренние силовые факторы в элементах конструкций статически неопределенной системы на основе метода сечений. Если степень статической неопределенности равно n, то система канонических уравнений выглядит:

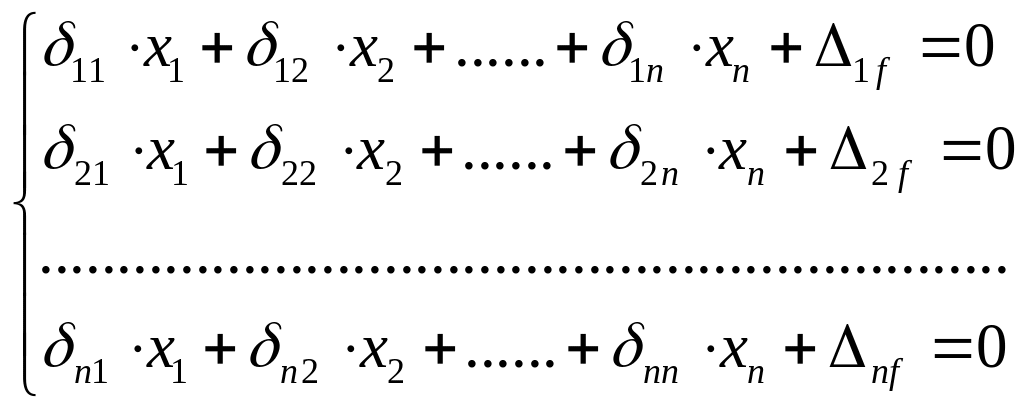
53. Матрица податливости. Механический смысл коэффициентов матрицы податливо­сти, приемы вычисления коэффициентов.

В расчетах на прочность и жесткость статически неопределимых систем широко используются метод сил и метод перемещений. Напомним, что для определения внутренних усилий в стати­чески неопределимых системах недостаточно лишь уравнений стати­ки: требуется составлять дополнительные уравнения деформаций (перемещений). Причем, если степень статической неопределимости невысока, то предпочтение обычно отдают первому методу, в про­тивном случае - второму.

Канонические уравнения метода сил (название указывает на то, что они составляются по определенному правилу - канону), в раз­вернутом виде записываются так :

δ₁₁X₁ + δ₁₂X₂+...+δ_1nХ_п +∆_1f =0;

δ_2lX_l+δ₂₂X₂ +...+δ_2nX_n+∆_2f=0;

………………………………….

δ _nlX_l + b_n2X₂ +... + b_nnX_n + ∆_nf = 0,

а в векторно-матричной форме

[δ]{X} + {∆_f} = {0},

г де квадратная матрица коэффициентов [δ] называется матрицей податливости конструкции. Она оказывается весьма удобной для описания упругих свойств конструкции, моделируемой в динамических расчетах системой с конечным числом степеней свободы. Коэффициент δ_ij представляет собой перемещение (линейное или угловое) по направлению i, вызванное силовым фактором (безразмерной силой или моментом соответственно), равным единице и действующим в направлении j. Очевидно, что эти коэффициенты можно определить по методике: предварительно строим эпюры изгибающих моментов M_t от единичных силовых факторов, действующих по направлениям, предоставленным степенями свободы системы. Количество эпюр равно и, т.е. по числу степеней свободы. Значение коэффициента δ_ij получается путем перемножения эпюр М_i и M_j. При постоянной жесткости (изгибной, на кручение и т.п.) отдельных участков конструкции целесообразно использовать способ Верещагина. В общем случае для плоских систем необходимо применять формулу Мора, удерживая в ней все три слагаемых или некоторые из них, в зависимости от требуемой точности решения. В динамических задачах {X}^T={X₁,…. Х_п}^Т - вектор-столбец внешних силовых факторов, {∆_f}^T = {∆_1f,… ∆_nf}^T- вектор-столбец перемещений; Т - знак транспонирования, использован для удобства записи столбцов в виде строк; соответственно X_i - i-й силовой фактор, а ∆_ij - перемещение в направлении i-й степени свободы, вызванное действи­ем заданной нагрузки. В задачах статического расчета статически не­определимых систем X_i - реакция в i-й связи, ∆_if - перемещение по направлению связи i, а механический смысл уравнений - отсут­ствие (отрицание) перемещений по направлениям жестких связей.