47. Теорема о взаимности работ(теорема Бетти)

Теорема о взаимности работ. Эта теорема вытекает из принципа независимости действия сил и применима ко всем системам, для кото­рых соблюдается этот принцип.

Рассмотрим линейно-упругую деформацию тела, закрепленного так, что исключены его смещения как жесткого тела, под действием сил F1, F2, приложенных в точках 1 и 2

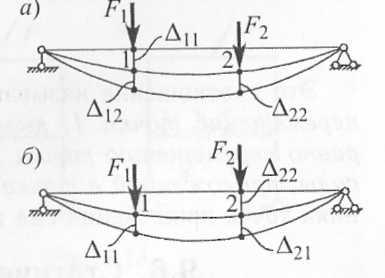
Перемещения точек тела будем обо­значать символом Δ с двумя индекса­ми. Первый индекс указывает место и направление перемещения, второй ин­декс — причину, вызвавшую это пере­мещение. Например, Δ12 — перемеще­ние точки 1 по направлению силы F1 от действия силы F2 ; Δ11 — перемещение по направлению силы F1 от действия этой же силы. Пусть сначала тело нагружается силой F1 .Эта сила совершит при своем возрастании от нуля до конечного значения ра­боту 1/2F1 Δ11 .Далее приложим к телу силу F2. Она совершит работу 1/2F2 Δ22

Но по мере роста этой силы точка 1 также получит переме­щение Δ 12, на котором сила F1 произведет работу F1 Δ12 .Всего в результате суммарного нагружения силы F₁ и F2 совершат работу (1)

которая накопится в виде потенциальной энергии деформации.

Изменим порядок нагружения, т.е. приложим сначала силу F2, а потом F₁. Тогда они произведут работу (2)

которая также перейдет в потенциальную энергию деформации.

Так как при упругой деформации конечное напряженно-деформи­рованное состояние не зависит от порядка приложения нагрузок, то два выражения (1) и (2) для потенциальной энергии деформа­ции тела в конечном состоянии должны быть равны. Сравнивая их, видим, что

Полученное равенство означает, что работа первой силы на переме­щении точки ее приложения, вызванном действием второй силы, равна работе второй силы на перемещении точки ее приложения под действием первой силы.

Это утверждение и составляет содержание теоремы о взаимности работ. Ее часто называют теоремой Бетти ').

Теорема Бетти становится более общей, если учесть, что здесь, как и при выводе теоремы Кастилиано, под F₁ и F₂ можно понимать не просто силы, а обобщенные силы, а под Δ12 и Δ21 — обобщенные перемещения.

47. Теорема о взаимности перемещений (теорема Максвелла)

Теорема о взаимности перемещений. Если силы F₁ и F2 равны по величине, то из

следует, что

Это соотношение называют теоремой о взаимности перемещений:

Теорема: перемещение точки приложенной силы на ее направленное вызванное действие второй единичной силы равно перемещению точки приложенной второй единичной силы по направлению последней, вызванной первой единичной силой.

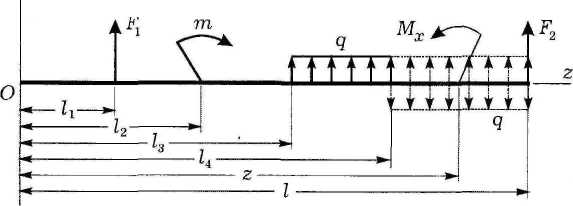
48. Метод начальных параметров. Рассмотрим балку постоянной жесткости, на которую действуют различные виды нагрузок (рису­нок 5.27) . Опоры отброшены, их действие заменено опорными реак­циями. Условимся:

1) начало координат помещать на левом конце балки;

2) сосредоточенный момент т привязывать к своему сечению, т. е. представлять в виде произведения m(z - а)0, где а - расстояние от начала координат до сечения, в котором момент приложен;

3) распределенную нагрузку, не доходящую до правого конца бал­ки, продолжать до этого конца, одновременно уравновешивая противоположно направленной нагрузкой той же интенсивности;

4) интегрирование выражений для изгибающего момента содержащих скобки проводить без раскрытия скобок

Выполнение перечисленных условий позволяет ограничиться составлением и интегрированием всего лишь одного дифференциального уравнения — уравнения последнего (крайнего правого) участка балки. В результате этого всегда образуются две константы интегрирования независимо от количества участков.

Уравнение для любого промежуточного участка может быть по­лучено из общего уравнения путем исключения слагаемых, которые содержат нагрузки, приложенные правее рассматриваемого участка.

Таким образом, при определении перемещений методом начальных параметров следует учитывать только те нагрузки, которые рас­положены слева от рассматриваемого сечения.

Левый конец балки совместим с началом координат. Используя метод сечений, составим выражение для изгибающего момента М_х на последнем, пятом, участке балки:

Здесь распределенная нагрузка продолжена до конца балки и снизу введена соответствующая компенсация. Это сделано для того, что­бы момент М_х на других участках балки можно было получить из соотношения (5.29), отбрасывая все нагрузки, расположенные правее сечения. Поэтому все распределенные нагрузки должны заканчиваться на правом конце балки. Сила F2 не входит в это уравнение, так как расположена правее рассматриваемого сечения.

Подставим полученное выражение для момента М_х в дифферен­циальное уравнение упругой линии балки:

При интегрировании этого выражения внешний момент будет привязывать к своему сечению: Тогда

Здесь θ, y0 -- константы интегрирования. Для выяснения их ме­ханического смысла рассмотрим крайнее левое сечение. Из выраже­ний, отбрасывая все нагрузки, расположенные правее сечения z = 0, получаем

;

Следовательно, величины θ₀ и у₀ являются углом поворота и проги­бом крайнего левого сечения балки. Поэтому их называют начальны­ми параметрами балки