1 Двойной интеграл в полярных координатах

Переход к полярным координатам частный случай замены переменных.

Луч, проходящий из произв точки О имеет на плоскости полярные координаты A(r, ) где r = |ОA| расстояние от О до А полярный радиус.  = угол между векторами ОА и ОР – полярный угол отсчитываемой от полярной оси против часовой стрелки. всегда 0<=r<=+, 0<= <=2 .

Зависимость между прямоугольными и полярными координатами: x = rcos , y = rsin .

Якобиан преобразования будет равен:

И формула при переходе примет вид:

15. Тройной интеграл.

Тройные интегралы

Пусть на некоторой ограниченной замкнутой области V трехмерного пространства задана ограниченная ф-ция f (x,y,z). Разобьем область V на n произвольных частичных областей, не имеющих общих внутренних точек, с объемами V1… Vn В каждой частичной области возбмем произв. точку М с кооорд Mi(i,i,i) составим сумму: f(i,i,i)Vi, кот наз интегральной суммой для ф-ции f(x,y,z). Обозначим за  максимальный диаметр частичной области. Если интегральная сумма при   0 имеет конечный предел, то сей предел и называется тройным интегралом от ф-ции f(x,y,z) по области V И обозначается:

Тройные интегралы. Опр. Св-ва. Вычисл.

Пусть на некоторой ограниченной замкнутой области V трехмерного пространства задана ограниченная ф-ция f (x,y,z). Разобьем область V на n произвольных частичных областей, не имеющих общих внутренних точек, с объемами V1… Vn В каждой частичной области возбмем произв. точку М с кооорд Mi(i,i,i) составим сумму: f(i,i,i)Vi, кот наз интегральной суммой для ф-ции f(x,y,z). Обозначим за  максимальный диаметр частичной области. Если интегральная сумма при   0 имеет конечный предел, то сей предел и называется тройным интегралом от ф-ции f(x,y,z) по области V И обозначается:

Св-ва такие же как у двойного интеграла.

Вычисление тройного интеграла в декартовых координатах. Пусть  является цилиндрическим телом, проекция которого на плоскость  есть область и которое ограничено снизу поверхностью , а сверху v поверхностью , где   - непрерывные функции в . Тогда , то есть интегрированием по z тройной интеграл сводится к двойному интегралу по области . Для областей более сложной формы вычисление двойных и тройных интегралов производится разбиением областей на конечное число простых областей с уже рассмотренными свойствами.

16. Тройной интеграл в сферических и цилиндрических координатах.

Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.

Если ограниченная замкнутая область пространства V = f(x,y,z) взаимно однозначно отображается на область V’ пространства = (u,v,w) Если непрерывно дифференцируемы функции: x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) и существует якобиан

то справедлива формула:

При переходе к цилиндрическим координатам, с вязанными с x,y,z формулами: x=rcos, y=rsin, z=z (0<=r<=+, 0<= <= 2, -<=z<=+)

Якобиан преобразования:

И поэтому в цилиндрических координатах переход осуществляется так:

При переходе к сферическим координатам: r?  , связанными с z,y,z формулами x=rsincos,

y=r sinsin, z=rcos.

(0<=r<=+, 0<= <= 2,

0<= <=2)

Якобиан преобразования:

Т. е. |J|=r²sin.

Итак, в сферических координатах сие будет:

17. Скалярное поле. Произведения по направлению. Градиент и его смысл.

1. Скалярное произведение функций. Ортогональные системы функций. Пространство L2.

Функция f(x) называется кусочно-непрерывной на отрезке [a,b], если она непрерывна на этом отрезке, за исключением, если она имеет лишь конечное число точек разрыва первого рода (пределы справа и слева конечны и различны). Такие функции можно складывать и умножать на действительные числа и получать как результат снова кусочно-непрерывные на [a,b] функции.

Скалярным произведением двух кусочно-непрерывных на [a,b] функций f и φ будем называть интеграл

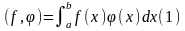
Очевидно, что для любых кусочно-непрерывных на [a,b] функциях f, φ, ψ выполняются свойства:

1. (f, φ) = (φ, f)

2. (f, f) ≥ 0 и из равенства (f, f)=0 следует, что f(x)=0 на [a,b], исключая лишь конечное число точек x

3. (αf + βφ, ψ)=α(f,φ) + β(f,ψ), где α и β – произвольные действительные числа.

Множество всех кусочно-непрерывных функций, определяемых на отрезке [a,b], для которых введено скалярное произведение по формуле (1), мы будем обозначать .

Из свойств 1, 2, 3 вытекает важное неравенство Буняковского

Функция называется нормальной, если

Две функции называются ортогональными (между собой) если (φ,ψ)=0. Система кусочно-непрерывных на отрезке [a,b] функций конечная или бесконечная называется ортогональной если функции имеют положительную норму и попарно ортогональны.

Система (1) называется ортогональной и нормальной (ортонормированной), если:

т.е. она ортогональна и каждая входящая в нее функция имеет единичную норму.

Любая конечная ортогональная система функций линейно независима в , т.е. из того что , где αk – числа, следует, что αk=0. В самом деле, если помножить обе части этого равенства скалярно на , то на основании линейных свойств скалярного произведения получим и т.к.

Производная по направлению и градиент скалярного поля. Пусть   - единичный вектор с координатами  ,  - скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле  . Производная по направлению представляет собой скалярное произведение вектора  и вектора с координатами  , который называется градиентом функции  и обозначается  . Поскольку  , где  - угол между  и  , то вектор указывает   направление скорейшего возрастания поля , а его модуль равен производной по этому направлению. Так как компоненты градиента являются частными производными, нетрудно получить следующие свойства градиента:

18. Векторное поле. Циркуляция. Линейный интеграл. Дивергенция и ротор, их вычисления. Потенциальное поле.