Комплексная форма ряда Фурье

Как известно из курса алгебры, экспонента от чисто мнимого аргумента определяется равенством .Отсюда немедленно вытекают формулы Эйлера 

справедливые для всех вещественных чисел .

Предполагая, что функция f разлагается в ряд Фурье, заменим в нем синусы и косинусы по формулам Эйлера:

где использованы обозначения

Вновь используя формулы Эйлера, преобразуем выражения для коэффициентов c_n:

Итак, мы видим, что для всех значений n коэффициенты c_n ищутся по одной формуле

При этом имеет место разложение

называемое комплексной формой ряда Фурье

9. Степенной ряд. Ряд Тейлора-Макларена. Разложение основных элементарных функций в ряд Тейлора-Макларена.

Разложение ф-ций в степенные ряды. Ряды Тейлора и Маклорена.

Пусть (1) сходится при |x-x0|<R а его сумма является ф-лой f(x)= (2) В этом случае говорят, что ф-ция f(x) разложена в степенной ряд. (1) .

Т1 Если ф-ция f распространяется в некоторой окрестности т. х0 f(x)= , то

и справедлива формула: (15) Если в некоторой окрестности заданной точки ф-ция распадается в степенной ряд, то это разложение единственно.

Пусть дествит. ф-ция f определена в некоторой окрестности т. х0 и имеет в этой точке производные всех порядков, тогда ряд: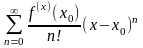 (6) наз рядом Тейлора ф-ции f в т, х0

При х0=0 ряд Тейлора принимает вид:

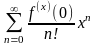(6’) и называется ряд Маклорена.

Ряд Тейлора может:

1 Расходится всюду, кроме х=х0

2 Сходится, но не к исходной ф-ции f(x), а к какой-нибудь другой.

3 Сходится к исходной ф-ции f(x)

Бесконечная дифференцируемость ф-ции f(x) в какой-то т. х0 является необходимым условием разложимости ф-ции в ряд Тейлора, но не является достаточным. Для введения дополнительных условий треб. ф-ла Тейлора.

Т2 Если ф-ция f(x) (n+1) раз дифференцируема на интервале (x0-h, x0+h) h>0, то для всех x  (x0-h, x0+h) имеет место ф-ла Тейлора:

где остаток r_n(x) можно записать:

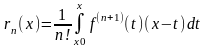(8)

(9) Формула (8) наз остаточным членом ф-лы Тейлора в интегральной форме. Ф-ла (9) – формулой Лагранжа.

Преобразуя ф-лу Тейлора при х0 = 0 получаем ф-лу Маклорена.

Т3 Если ф-ция f(x) имеет в окрестности т х0 производные любого порядка и все они ограниченны одним и тем же числом С, т е  x  U(x0) |f⁽ⁿ⁾(x)|<=C, то ряд Тейлора этой ф-ции сходится в ф-ции f(x) для всех х из этой окрестности.

28. Ряд Тейлора и ряд Лорана.

Тейлор: Если в точке z₀ f(z) аналитична, то в окрестности этой точки она представима рядом

где Г- окружность с центром в точке z=z₀ , целиком лежащая в окрестности точки z₀ , в которой функция f(z) аналитична.

Лоран (о разложении функции в ряд по целым степеням).

Функция f(z), аналитическая в кольце r < | z - z₀ | < R,    представляется в этом кольце сходящимся рядом по целым степеням, т.е. имеет место равенство:          (1)

Коэффициенты ряда вычисляются по формуле: (2) где - произвольный контур, принадлежащий кольцу и охватывающий точку z₀; в частности, - окружность  

Ряд (1), коэффициенты которого вычисляются по формуле (2), называется рядом Лорана функции f(z).

Совокупность членов ряда с неотрицательными степенями  называется правильной частью ряда Лорана, члены с отрицательными степенями образуют главную часть ряда Лорана:  или  

Для коэффициентов ряда имеет место формула оценки коэффициентов - неравенство Коши:  где   r  -  радиус контура интегрирования в формуле (2).

На границах кольца сходимости ряда Лорана есть хотя бы по одной особой точке функции f(z) - его суммы.

Частными случаями рядов Лорана являются разложения функции в окрестности особой точки z₀ (r = 0) и в окрестности бесконечно удаленной точки (z₀ = 0, ).

При построении разложений в ряд Лорана используются разложения в степенные ряды (ряды Тейлора), используются основные разложения и арифметические операции со сходящимися рядами

10. Приложение степенных рядов. Вычисления значения функций определенных интегралов. Решение задачи Коши для дифференциальных уравнений.

Диффиренцируемость. Коши-Риман.

Пусть w = f(z) определена, однозначна и принимает собственные значения в окрестности точки z = x + iy ∈ C. Производной функции w = f(z) в точке z называется предел . Функция, имеющая конечную производную в точке z, называется дифференцируемой в этой точке.         В этом определении важно, что стремление Δz → 0 может проходить по любому пути. Как мы увидим дальше, вследствие этого обстоятельства существование производной f’(z) не сводится к существованию частных производных функций u(x, y) и v(x, y), а требует некоторых дополнительных условий. Сейчас мы дадим определение основного в теории ФКП понятия - аналитичности функции в точке и в области.         Определение. Однозначная функция называется аналитической (регулярной, голоморфной) в точке z, если она дифференцируема в некоторой окрестности этой точки.          Однозначная функция называется аналитической в области D, если она аналитична в каждой точке этой области.

Условие Коши-Римана.

Теорема: если  производная f^/(z), то выполняется условие =>

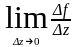
Доказательство: Пусть  f^/(z)<=>

По любому направлению z->0 и не зависит от этого стремления. z=x+iy=> в частности, z=x->0 и z=iy->0, т.е. по направлению ||Ox или || Oy

12. Формула Эйлера (вывод с использованием рядов).

Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту стригонометрическими функциями.

Формула Эйлера утверждает, что для любого вещественного числа   выполнено следующее равенство:

,

где   — основание натурального логарифма,

 — мнимая единица.

Доказательство формулы Эйлера можно провести с использованием рядов Тейлора. Разложим функцию   в ряд Тейлора по степеням  . Получим:

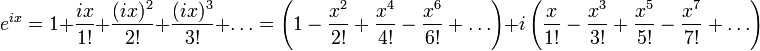
Но

Поэтому 

ч. т. д.

13. Двойной интеграл. Свойства. Смысл. Приложения. Вычисления с помощью двукратного интегрирования в декартовых координатах.

Двойной интеграл

Рассмотрим в плоскости Оху замкнутую область D, ограниченную линией Г, являющейся замкнутой непрерывной кривой. z = l(P) = f(x,y), P= (x,y)  D – произвольные ф-ции определенные и ограниченные на D. Диаметром области D наз. наибольшее расстояние между граничными точками. Область D разбивается на n частых областей D1…Dn конечным числом произв. кривых. Если S – площадь D, то Si – площадь каждой частной области. Наибольший из диаметров областей обозн . В каждой частной области Di возьмем произв. точку Pi (i , Di)  Di, наз. промежуточной. Если диаметр разбиения D   0 , то число n областей Di  . Вычислим зн-ие ф-ции в промежуточных точках и составим сумму:I = 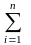f(i, Di)Si (1), наз. интегральной суммой ф-ции. Ф-ция f(x,y) наз. интегрируемой в области D если существует конечный предел интегральной суммы.

Двойным интегралом ф-ии f(x,y) по области D наз. предел интегральной суммы при   0. Обозн:

или

Условие существования двойного интеграла .Необходимое, но недостаточное:

Ф-ция f(x,y) интегрируема на замкнутой области D, ограничена на D.

1 достаточный признак существования: если ф-ция f(x,y) непрерывна на замкнутой, огр. области D, то она интегрируема на D.

2 достаточный признак существования: если ф-ция f(x,y) ограничена в замкнутой области D с какой-то границей и непрерывна в ней за исключением отдельных точек и гладки=х прямых в конечном числе где она может иметь разрыв, то она интегрируема на D.