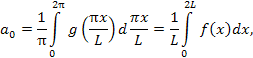- •2 Необходимый признак сходимости рядов
- •Комплексная форма ряда Фурье
- •Двойной интеграл. Опр. Св-ва. Вычисление.
- •1 Двойной интеграл в полярных координатах
- •Тройные интегралы
- •Тройные интегралы. Опр. Св-ва. Вычисл.
- •Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
- •Векторные поля к простейшим векторным полям относятся: соленоидальное, потенциальное игармоническое.
- •Циркуляция векторного поля
1.Числовой ряд. Сходимость и расходимость. Признак сходимости. Необходимый остаток ряда, приближенное вычисление суммы сходящегося ряда с заданной погрешностью.
Понятие числового ряда и его суммы
Пусть задана бесконечная последовательность чисел u1, u2, u3…
Выражение u1+ u2+ u3…+ un (1) называется числовым рядом, а числа его составляющие- членами ряда.
Сумма конечно числа n первых членов ряда называется n-ной частичной суммой ряда: Sn = u1+..+un
Если сущ. конечный
предел:
 ,
то его называют суммой ряда и говорят,
что ряд сходится, если такого предела
не существует, то говорят что ряд
расходится и суммы не имеет.
,
то его называют суммой ряда и говорят,
что ряд сходится, если такого предела
не существует, то говорят что ряд
расходится и суммы не имеет.
2 Необходимый признак сходимости рядов
Если ряд сходится, то
предел его общего члена равен нулю:
Док-во:

Sn=u1+u2+…+un
Sn-1\u1+u2+…+un-1
un=Sn-Sn-1, поэтому:

Сей признак является только необходимым, но не является достаточным., т. е. если предел общегоь члена и равен нулю совершенно необязательно чтобы ряд при этом сходился. Следовательно, вот сие условие при его невыполнении является зато достаточным условием расходимости ряда.
2. Знакоопределенные ряды. Теорема сравнения предельного признака сравнения. Признаки Даламбера и Коши (док-во).
Признаки сравнения
Т(Признаки сравнения)
Пущай
 и
и
 ряды с неотрицательными членами и для
любого n выполняется
нер-во:
ряды с неотрицательными членами и для
любого n выполняется
нер-во:
un<=vn (1)тогда
1 Если ряд vn сходится, то сходится и ряд un
2 если ряд un расходится, то расходится и ряд vn. Т. е. говоря простыми русскими словами для простых русских людей (ну для дураков вроде тебя): Из сходимости ряда с большими членами следует сходимость ряда с меньшими, а из расходимости ряда с меньшими членами следует расходимости ряда с большими и не наоборот!!!
Причем можно требовать, чтобы неравенство (1) выполнялось не для всех номеров n, а начиная с некоторого n0, т. е. для некоторых номеров меньших n0 неравенство (1) может и не выполняться. При применении сего признака сравнения удобно в качестве ряда сравнения брать ряд Дирихле или геометрический ряд, с которыми и так уже все ясно.
Т3 Засекреченная
Если сущ вышеописанные неотр. ряды, то если сущ предел:
 (0<k<+)
тада оба эти ряда сходятся.
(0<k<+)
тада оба эти ряда сходятся.
Предельный признак сравнения
Пусть
даны два знакоположительных числовых
ряда
![]() (7) и
(7) и
![]() (8). Если существует конечный предел
(8). Если существует конечный предел ![]() ≠0,
то ряды
(7) и
(8) сходятся или расходятся одновременно.
≠0,
то ряды
(7) и
(8) сходятся или расходятся одновременно.
Доказательство. По условию теоремы
существует конечный предел
.
Это означает, что для любого положительного
числа Е существует такой номер N,
что для всех номеров n≥Nвыполняется
условие ![]() Последнее
неравенство равносильно двойному
неравенству –E<
Последнее
неравенство равносильно двойному
неравенству –E<![]() -A<E или A-E<
-A<E или A-E<![]() <A+E или
<A+E или
![]() (9)
(9)
Неравенство (9) верно при любом E>0.
Выберем поэтому Е так, чтобы
выполнялось А-Е>0. Если ряд (8) сходится,
то сходится и ряд ![]() по
теореме 2. Но тогда по признаку сравнения,
учитывая (9), сходится и ряд
(7). Если ряд
(7) сходится, то по признаку сравнения,
учитывая (9), сходится ряд
по
теореме 2. Но тогда по признаку сравнения,
учитывая (9), сходится и ряд
(7). Если ряд
(7) сходится, то по признаку сравнения,
учитывая (9), сходится ряд ![]() и
по теореме 2 сходится ряд
(8). Аналогично доказывается, учитывая
(9), что из расходимости одного из рядов
следует расходимость другого ряда.
Докажите эту часть самостоятельно.
и
по теореме 2 сходится ряд
(8). Аналогично доказывается, учитывая
(9), что из расходимости одного из рядов
следует расходимость другого ряда.
Докажите эту часть самостоятельно.
Замечание. Предельный признак сравнения рекомендуется применять в тех случаях, когда общий член ряда представляет собой отношение степенных функций. Для сравнения выбирается обобщённый гармонический ряд, общий член которого равен отношению старших степеней числителя и знаменателя общего члена данного ряда.
Пример.
Исследовать на сходимость ряд ![]() Здесь un=
Здесь un=![]()
Возьмём для сравнения ряд с общим
членом vn=![]() то
есть расходящийся гармонический
ряд
то
есть расходящийся гармонический
ряд ![]() Применим
предельный признак сравнения.
Применим
предельный признак сравнения.
![]()
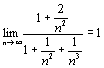 0,
0,
следовательно, данный ряд расходится по предельному признаку сравнения.
Признак Даламбера
Пусть дан знакоположительный числовой ряд
![]() (7)
(7)
и пусть существует предел ![]() При p<1
ряд (7) сходится, при p>1
ряд (7) расходится.
При p<1
ряд (7) сходится, при p>1
ряд (7) расходится.
Доказательство. По условию существует
предел ![]() .
Это означает, что для любого положительного
числа Е существует такой номер N,
что для всех номеров nN выполняется
условие
.
Это означает, что для любого положительного
числа Е существует такой номер N,
что для всех номеров nN выполняется
условие![]() или
или
p-E<![]() (10)
(10)
Пусть сначала p<1.
Выберем Е так, что p+E=q<1. Для
всех nN имеем ![]()
![]()
![]() …
или
…
или
![]()
или
![]() (11)
(11)
Рассмотрим ряды
![]() (12)
(12)
![]() . (13)
. (13)
Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.
Пусть теперь p>1.
Выберем Е так, что p-E>1.
Тогда из левой части неравенства (10)
следует, что при nN выполняется ![]() или un+1>un,
то есть члены ряда возрастают с
возрастанием номера n.
Поэтому
или un+1>un,
то есть члены ряда возрастают с
возрастанием номера n.
Поэтому ![]() un0,
следовательно, ряд расходится по
следствию из необходимого признака
сходимости. Теорема доказана.
un0,
следовательно, ряд расходится по
следствию из необходимого признака
сходимости. Теорема доказана.
Замечания.
1. Если расходимость ряда установлена с помощью признака Даламбера, то un0.
2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.
3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.
Пример.
Исследовать на сходимость ряд ![]()
Применим признак
Даламбера. un=![]() un+1=
un+1=![]() =
=
![]() .
. ![]()
 следовательно,
ряд сходится по признаку Даламбера.
следовательно,
ряд сходится по признаку Даламбера.
Теорема 7. (Признак Коши)
Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)
и пусть существует предел ![]() При p<1
ряд (7) сходится, при p>1
ряд (7) расходится.
При p<1
ряд (7) сходится, при p>1
ряд (7) расходится.
Доказательство. По условию существует
Это
означает, что для любого положительного
числа Е существует такой номер N,
что для всех nN выполняется
условие ![]() <E или
<E или
p-E<![]() <p+E. (14)
<p+E. (14)
Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем <q или un<qn для всех nN. Рассмотрим ряды
![]() (15)
(15)
![]() (16)
(16)
Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un<qn для всех nN, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).
Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем >1 или un>1, следовательно, un0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.
Теорема 8. (Интегральный признак Коши)
Пусть члены знакоположительного
числового ряда u1+u2+…+un… (7)
не возрастают: u1u2≥…≥un≥…
и пусть f(x) такая
положительная, непрерывная, невозрастающая
на промежутке [1;∞) функция,
чтоf(1)=u1, f(2)= u2 ,…, f(n)=
=un,…
. Тогда ряд (7) сходится или расходится
одновременно с несобственным интегралом ![]()
3. Признак Лейбница. Оценка остатка ряда удовлетворяющего признаку Лейбница.
Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится.
Или в два пункта:
1) Ряд является знакочередующимся.
2)
Члены ряда убывают по модулю: ![]() .
Причём, убывают монотонно.
.
Причём, убывают монотонно.
Если выполнены оба условия, то ряд сходится.
Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
![]()
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
Пусть для знакочередующегося ряда
выполняются следующие условия:
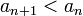 (монотонное
убывание {an})
(монотонное
убывание {an}) .
.
Тогда этот ряд сходится
Пример
![]() .
Ряд из модулей имеет вид
.
Ряд из модулей имеет вид ![]() —
это гармонический
ряд,
который расходится.
—
это гармонический
ряд,
который расходится.
Теперь воспользуемся признаком Лейбница:
знакочередование выполнено


 .
.
Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно. Оценка остатка ряда Лейбница .Из доказательства признака Лейбница следует, что сумма знакопеременного сходящегося ряда меньше по модулю первого члена остатка ряда. Поскольку любой остаток ряда rn является также рядом Лейбница, то для него справедливо:
![]() .
.
4. Абсолютная сходимость ряда. Теорема об абсолютной сходимости. Условная сходимость.
Знакопеременные ряды.
Абсолютная и условная сходимость рядов.
Ряд называют знакопеременным, если его членами являются действительные числа, а знаки его членов могут меняться как кому в голову взбредет. Пусть дан ряд:
u1+u2…+un= (1), где un – может быть как положительным, так и отрицательным. Рассмотрим ряд состоящий из абсолютных значений этого ряда:
|u1|+|u2|…+|un|= (2),
(2),
Если сходится ряд (2), то ряд (1) называют абсолютно сходящимся, а вот если ряд (1) сходится, а ряд (2) расходится. то ряд (1) наз сходящимся условно.
Т. Признак абсолютной сходимости:
Если знакочередующийся ряд сходится условно. то он и просто так сходится, при этом:
 <=
<=
Доквы:
т. к. 0<=|un|+un<=2|un|, то по признаку сравнения сходится ряд |un|+un, тогда сходится ряд: (|un|+un)-|un|=un. Далее, т. к. по св-ву абсолютной величины |Sn|=|u1+u2+…+un|<=|un| n N, то переходя к пределу получим:
<=
Т2 Если ряд (1) абсолютно сходится, то и любой ряд составленный из тех же членов, но в любом другом порядке тоже абсолютно сходится и его сумма равна сумме ряда un – Sn. А вот с условно сходящимися рядами все гораздо запущенней.
Т(Римана)
Если знакопеременный ряд с действительными членами сходится условно, то каким бы ни было дейст. число S можно так переставить члены ряда, что его сумма станет равна S, т. е. сумма неабсолютно сходящегося ряда зависит от порядка слагаемых
5. Ряды
Фурье для функции с периодом

Ряд Фурье для периодической функции с периодом T = 2L |
|
|
|
Пусть g (x) – периодическая функция с периодом 2π:
Тогда функция
Следовательно, для
разложения периодической функции
f (x) с периодом 2L в ряд Фурье
можно использовать соответствующие
формулы для периодической функции с
периодом 2π, выполнив в них подстановку
Аналогичным образом обобщаются формулы для ряда и коэффициентов Фурье в комплексной форме на случай периодической функции f (x) с периодом 2L:
|
6. Ряд
Фурье четной функции, разложение по

f(t) – четная на [-a;a], a>0

7. Ряд
Фурье нечетной функции, разложение по

Разложение в ряд Фурье четных и нечетных функций.
f(t) – четная на [-a;a], a>0
8. Ряд Фурье в комплексной форме