14. Динамика вращательного движения абсолютно твердого тела. Момент силы. Работа при вращении абсолютно твердого тела вокруг неподвижной оси.

Пусть твердое тело вращается относительно оси под действием нескольких сил с суммарным моментом М относительно той же оси. Тогда работа этих сил приводит к изменению кинетической энергии этого тела.

, ,,

, ,

, ,

,

,

,

- основное уравнение динамики вращательного движения.

Момент силы относительно оси - проекция на эту ось вектора момента силы относительно любой точки, выбранной на данной оси.

Элементарная работа, совершаемая моментом силы, при вращательном движении относительно неподвижной оси вычисляется по формуле: (*).

Полная работа

Если , то

\\

15.Кинетическая энергия абсолютно твнрдого тела, вращающегося вокруг относительно неподвижной оси. Момент инерции. Теорема Штейнера. Моменты инерции тел простейшей геометрической формы.

Кинетическая энергия твёрдого тела, вращающегося относительно неподвижной оси.

Рассмотрим абсолютно твёрдое тело, вращающееся около неподвижной оси, проходящей через тело. Мысленно разобьём это тело на маленькие объёмы с элементарными массами m₁, m₂,…,m_n, находящиеся на расстоянии r₁, r₂,…, r_n, от оси вращения. При вращении твёрдого тела относительно неподвижной оси отдельные его элементарные объёмы опишут окружности различных радиусов r_i и имеют различные линейные скорости υ_i. Кинетическую энергию вращающегося тела найдём как сумму кинетических энергий его элементарных объёмов.

T_вр=∑ⁿ_i=1m_iυ_i²/2=∑ⁿ_i=1m_iω²r_i²/2=(ω²∑ⁿ_i=1m_ir_i²)/2=I_zω²/2, 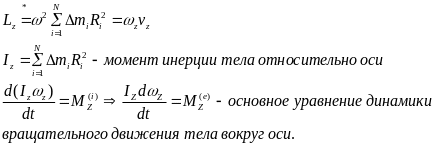где I_z – момент инерции тела. Вращение твёрдого тела вокруг неподвижной оси:

Можно показать, что проекция момента импульса на ось “Z” может быть записана таким образом:

где R – расстояние до оси.

Момент инерции материальной точки относительно неподвижной оси - скалярная физическая величина, являющаяся мерой инертности этой точки при вращательном движении и, равная произведению её массы на квадрат расстояния до оси, т.е. , а также , где - угловая скорость тела относительно данной оси.

Теорема Штейнера: Момент инерции твердого тела относительно некоторой оси вращения равен сумме момента инерции этого тела относительно оси параллельной данной и проходящей через центр масс тел и произведению массы тела не квадрат расстояния между осями.

• Обруч

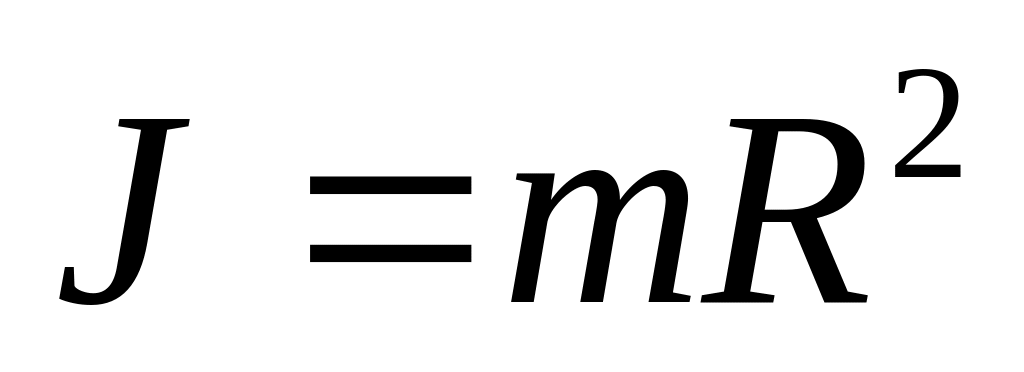
• Цилиндр

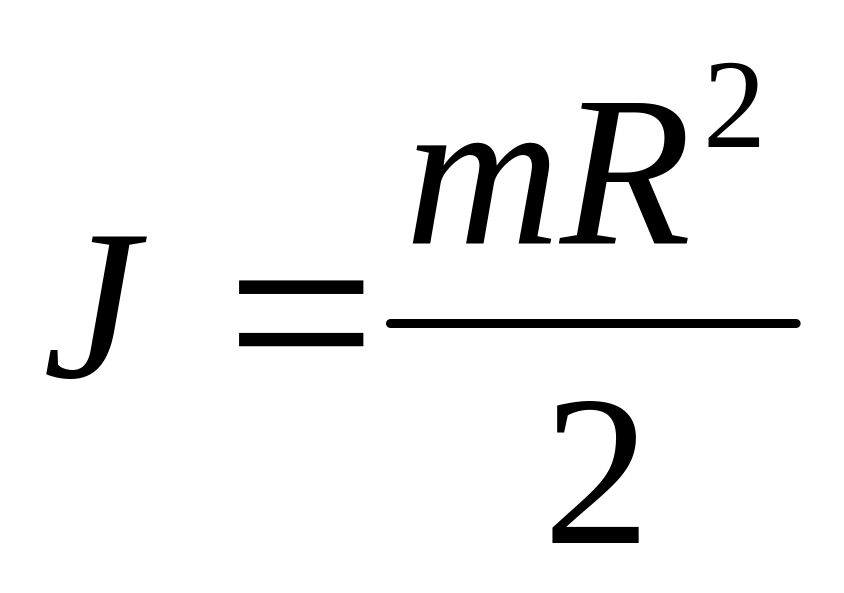
• Круг

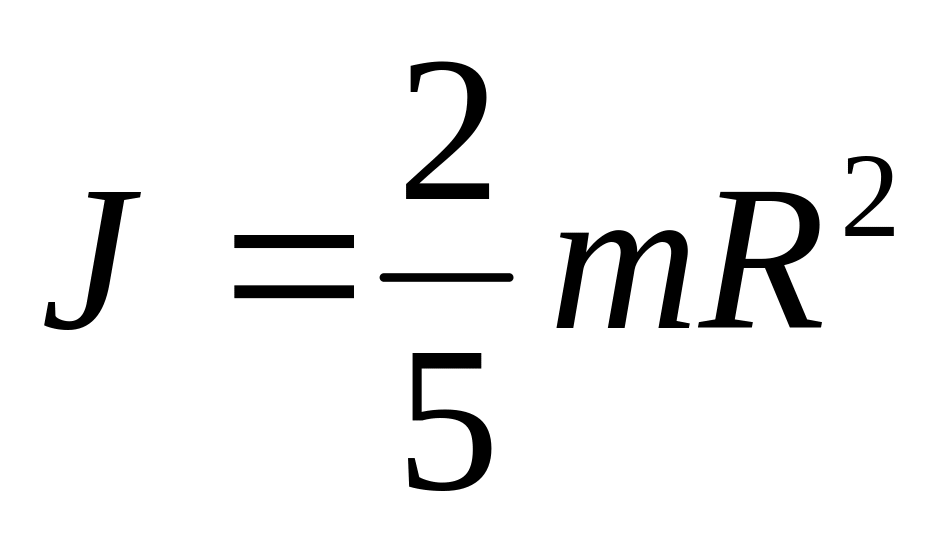
• Стержень, ось посередине

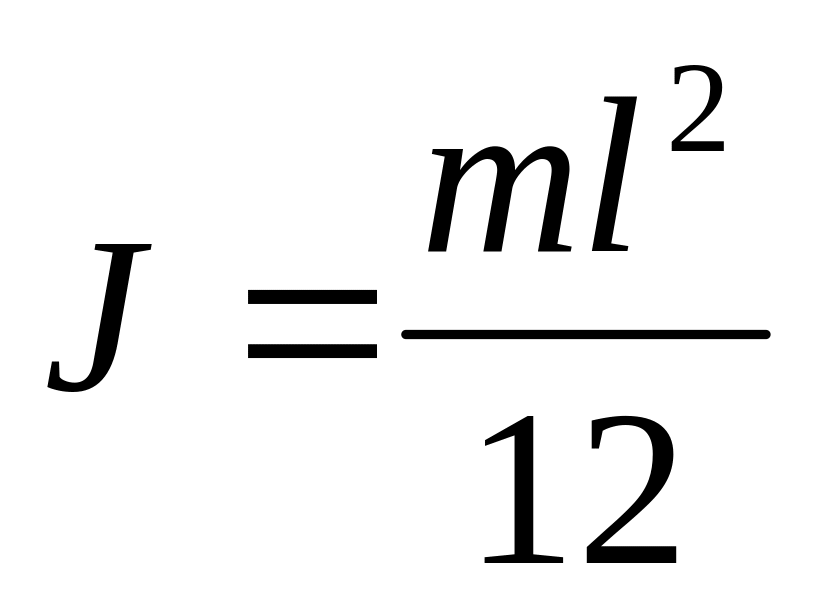
• Стержень, ось на конце

16. Вывод основного уравнения динамики вращательного движения абсолютно твердого тела. Момент импульса материальной точки и твердого тела. Закон сохранения момента импульса.

Формулировка закона: Скорость изменения момента импульса относительно полюса равна главному моменту силы относительно того же полюса, т.е.

В проекциях на оси координат: .

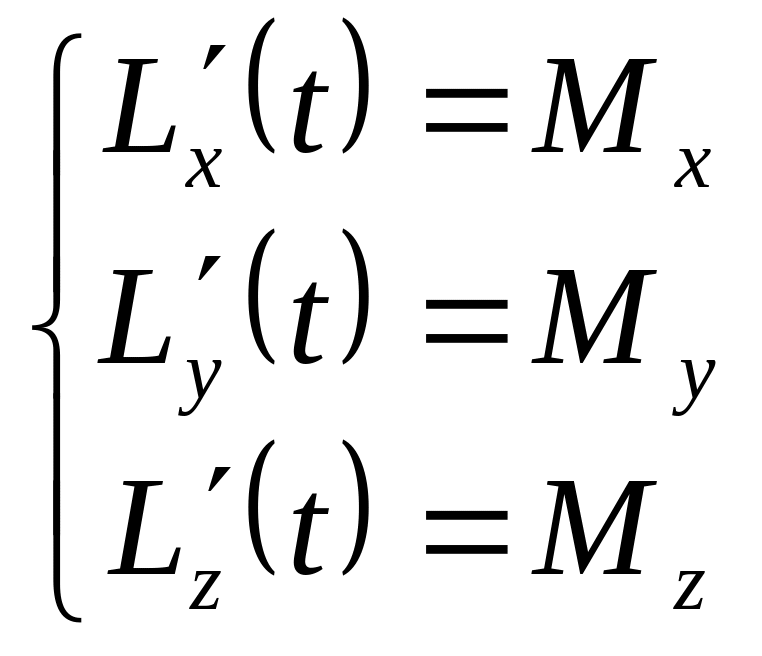Если вращение тела происходит относительно неподвижной оси, то основной закон динамики вращательного движения примет вид: . В данном случае момент импульса легко выразить через угловую скорость и момент инерции тела относительно рассматриваемой оси: . Тогда основной закон динамики вращательного движения примет вид: . Если тело не рассыпается и не деформируется, то

, вследствие чего . Если ко всему , то и, оно равно: .

Элементарная работа, совершаемая моментом силы, при вращательном движении относительно неподвижной оси вычисляется по формуле: (*). Полная работа Если , то На основании формулы (*), получим выражение для кинетической энергии вращательного движения твёрдого тела относительно неподвижной оси. Т.к. , то . После интегрирования, получим окончательный результат для кинетической энергии вращательного движения относительно неподвижной оси .

Момент импульса – псевдовекторная величина. Направление этого вектора находится по тому же правилу, сто и нахождение момента силы (вращение рукоятки буравчика по направлению вектора скорости)

Моментом импульса системы материальных точек относительно полюса называется векторная величина, равная векторной сумме моментов импульсов относительно полюса всех материальных точек системы, т.е. , где  масса, радиусвектор и скорость «i-ой» точки системы.

Моментом импульса материальной точки относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента импульса этой точки относительно произвольной точки данной оси.

Моментом импульса системы материальных точек относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента импульса системы относительно произвольной точки данной оси.

В частном случае вращательного движения точки по окружности, момент её импульса равен:

, где   угол между радиусом окружности и скоростью.

Физический смысл момента импульса: Момент импульса характеризует интенсивность вращательного движения.

закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчёта (относительно поворота замкнутой системы в пространстве на любой угол).