1. Пространство, время. Механическое движение. Система отсчета.

Пространство и время, философские категории. Пространство — форма сосуществования материальных объектов и процессов (характеризует структурность и протяженность материальных систем); время — форма и последовательные смены состояний объектов и процессов (характеризует длительность их бытия). Пространство и время имеют объективный характер, неразрывно связаны друг с другом, бесконечны. Универсальные свойства времени — длительность, неповторяемость, необратимость; всеобщие свойства пространства — протяженность, единство прерывности и непрерывности.

Механическое движение – это изменение с течением времени взаимного расположения тел и их частей.

Положение тела в пространстве можно определить только по отношению к другим телам.

Система отсчета – система координат, жестко связанная с абсолютно твердым телом, снабженная часами и используемая для определения положения в пространстве тел или их частей в любые моменты времени. Иногда система отсчета называют хронометрированной системой координат.

Тело отсчета – абсолютно твердое тело, с которым жестко связана система координат. Обычно это инерциальная система отсчета..

2.Киниматика материальной точки. Системы отсчета. Два способа описания движения материальной точки. Скорость и ускорение произвольно движущейся м.т. как производные радиуса вектора (первый способ описания движения).

Материальная точка – модель реального тела размерами, которого в данных условиях можно пренебречь. При этом масса тела считается сосредоточенной в геометрической точке.

Система отсчета – система координат, жестко связанная с абсолютно твердым телом, снабженная часами и используемая для определения положения в пространстве тел или их частей в любые моменты времени. Иногда система отсчета называют хронометрированной системой координат.

Тело отсчета – абсолютно твердое тело, с которым жестко связана система координат. Обычно это инерциальная система отсчета.

Описать движение материальной точки, значит указать положение этой точки в любой момент времени.

I Векторный способ.

Положение м.т. задается радиус вектором проведенным из некоторой неподвижной точки О в выбранной С.О. в т.М

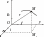- основной закон описания движения материальной точки.

Если найти эту зависимость то можно сказать что описали движение материальной точки.

II Координатный способ

С выбранным телом отсчета жестко связывают определенную систему координат. Запишим проекции на оси декартовой системы координат радиус-вектора r(t).

Зная зависимость этих координат от времени (закон движения м.т.) можно найти положение точки в каждый момент времени, а так же ее скорость и ускорение.

Скорость – векторная величина, которая определяет как быстроту движения, так и его направление в данный момент времени. Первая производная перемещения по времени.

Вектором средней скорости называется отношение приращения радиус-вектора точки к промежутку времени. <υ>=Δr/Δt.

М гновенная скорость – это векторная величина, определяемая производной радиус-вектора движущейся точки по времени. υ=lim_Δt→0Δr/Δt.

Мгновенная скорость – векторная величина, определяемая производной радиус-вектора движущейся точки по времени. υ=dr/dt.

Ускорение – это характеристика неравномерного движения; определяет быстроту изменения скорости по модулю и направлению. Вторая производная перемещения по времени.

Среднее ускорение неравномерного движения за промежуток времени – это векторная величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло. <a>=Δυ/Δt.

Мгновенным ускорением материальной точки в момент времени t будет предел среднего ускорения. a=dυ/dt.

Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории.) a_τ=dυ/dt.

Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению (направлена к центру кривизны траектории). a_n=υ²/r.