2. Основные теоретические положения

Триггеры разделяются на три основных класса: асинхронные потенциальные, асинхронные импульсные и синхронные.

Асинхронные потенциальные триггеры изменяют сове состояние под действием изменения амплитуды входных сигналов. Длительность воздействия этих сигналов значительно превосходит время переходных процессов в самом триггере.

Асинхронные импульсные триггеры характеризуются тем, что входные сигналы воздействуют на них лишь кратковременно в момент изменения из «I» в «0» или наоборот.

Синхронные триггеры кроме основных (информационных) входов имеют также вход для подачи тактового сигнала. Состояние синхронных триггеров может изменяться только под воздействием изменения дополнительного – тактового сигнала из «I» в «0», а основные сигналы могут только разрешать или запрещать это изменение.

В зависимости от функциональных возможностей триггеры подразделяются на: RS, D, T, У – К и другие триггеры.

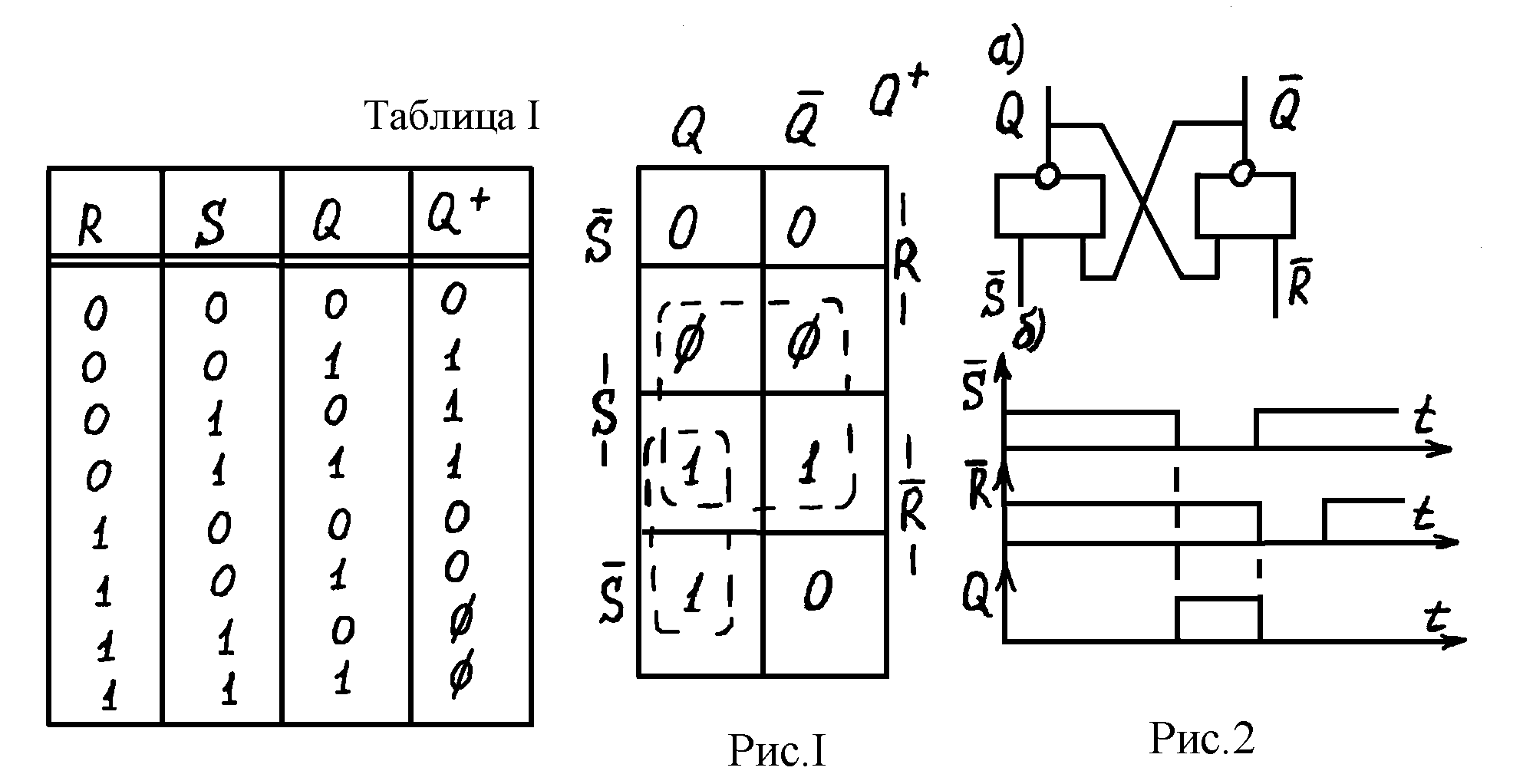
2.1. Асинхронный потенциальный RS-триггер

Асинхронный потенциальный RS-триггер имеет два входа R и S и два выхода – прямой и инверсный . Вход S предназначен для установки триггера в единичное состояние (Q=1), а вход R – для установки триггера в нулевое состояние (Q=0) – сброс. Одновременная подача сигналов R=S=1 запрещена. Закон функционирования триггера задается таблицей истинности (табл.1), в которой Q – выходной сигнал триггера в момент времени, предшествующий моменту подачи входных сигналов, а - выходной сигнал триггера в момент времени, следующий за моментом изменения входных сигналов. Сигнал является функцией входных сигналов R и S и предыдущего состояния триггера Q. Функция называется функцией переходов триггера. В таблице две последние строки соответствуют запрещенному состоянию входа R=S=1, поэтому в этих случаях функция не определена. По таблице истинности составляется диаграмма Вейча для функции (рис.1), из которой получаем ее выражение

, (1)

причем на входные сигналы накладывается ограничение, задаваемое уравнением RS=0. Для реализации уравнения (1) из элементов И – НЕ преобразуем выражение (1):

. (2)

Схема триггера, составленная по уравнению (2) представлена на рис.2,а, а временные диаграммы, поясняющие работу RS-триггера – на рис.2,б.

2.2. Синхронный D-триггер

D-триггер имеет один информационный вход D и вход для подачи тактового сигнала С. Выходной сигнал триггера принимает значение входного сигнала D в момент времени, когда тактовый сигнал С изменяется из «I» в «0», dC=I. Табл.2 задает закон функционирования D-триггера. Из диаграммы Вейча на Рис.3 получаем функцию переходов в виде

. (3)

D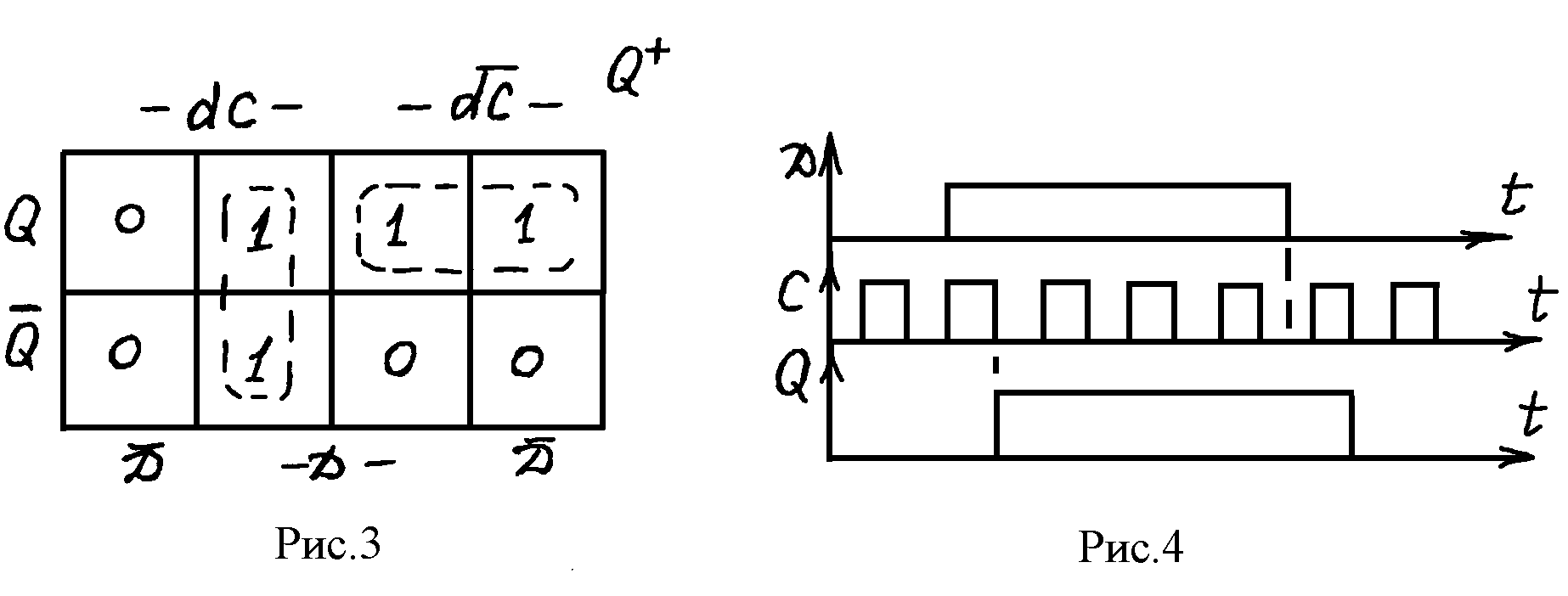 -триггер является синхронным элементом задержки входного сигнала D на один такт С (Рис.4). Из (3) следует, что входной сигнал D не должен изменяться в момент времени, когда dC=1, так как это привело бы к неопределенности переходов ( ø).

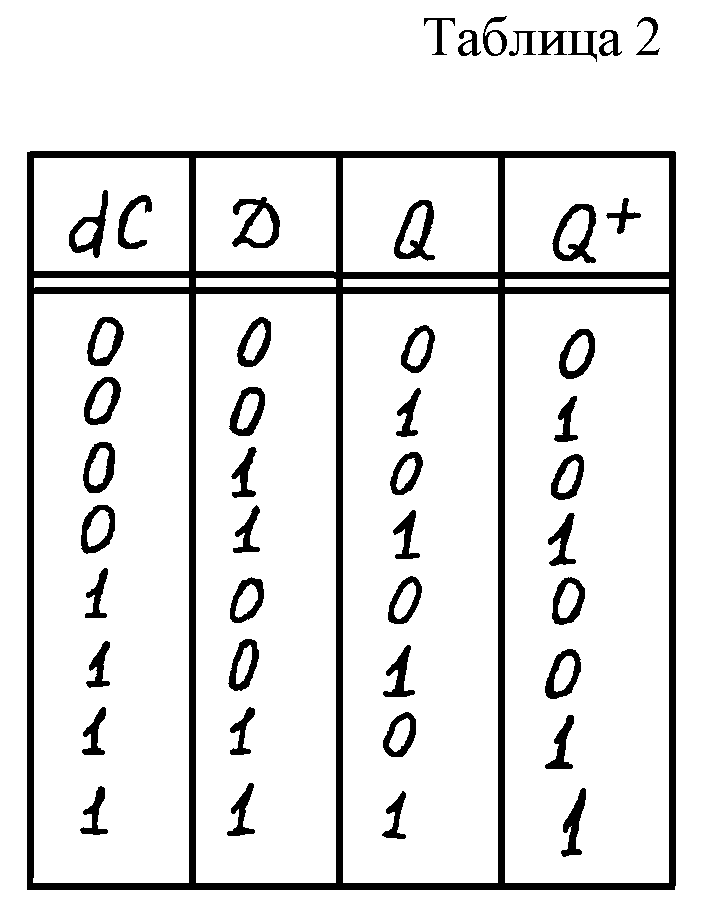
2.3. Асинхронный импульсный Т-триггер

Триггер типа Т имеет один выход Т и изменяет свое состояние при каждом изменении входного сигнала Т из «I» в «0». Преобразование потенциального сигнала в импульсный записывается с помощью перехода d. DT – обозначение импульсного сигнала. Составив таблицу истинности, задающую функцию переходов dT-триггера (Табл.3), получим:

. (4)

Временные диаграммы на рис.5 поясняют работу Т-триггера.

Из рис.5 видно, что сигнал на выходе Q имеет в два раза меньшую частоту, чем у входного сигнала Т. Следовательно, из Т-триггеров легко получить делители частоты сигнала на величину, кратную двум, а также асинхронные счетчики входных сигналов объемом памяти 2ⁿ , где n – число последовательно соединенных Т-триггеров.

Т-триггер легко получить из D-триггера (рис.6). Для этого достаточно вход соединить с выходом D, тогда с изменением каждого синхронизирующего импульса из «I» в «0» триггер будет изменять свое состояние на противоположное.

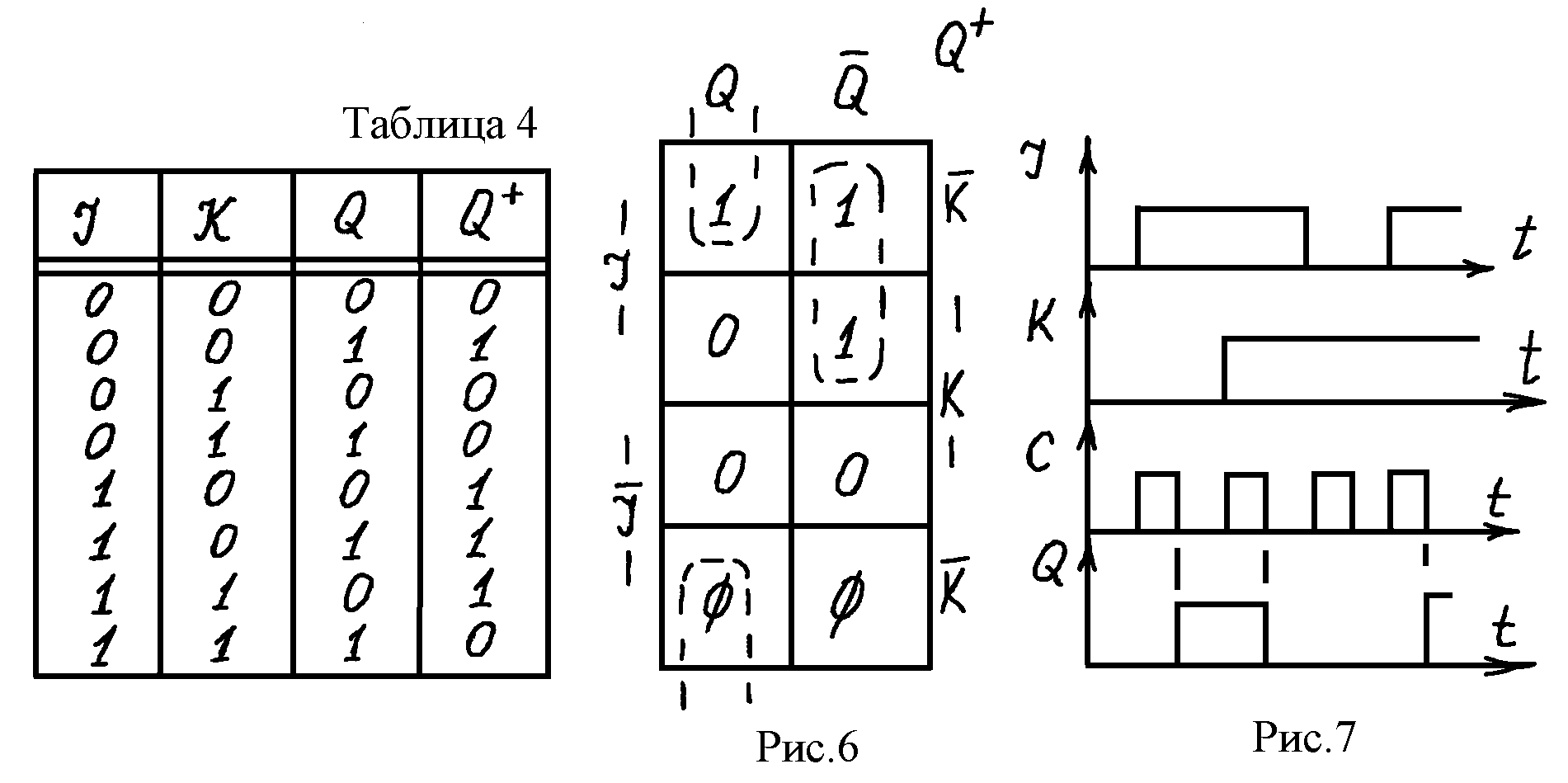
2.4. J-К-триггер

J-К-триггер имеет два информационных входа и вход тактового сигнала С. В дискретные моменты времени при J=I триггер устанавливается в состояние Q=I при К=I в состояние Q=0, а при J=К=1 в состояние = . На основании описанного закона функционирования переходов задается Табл.4. Составив по таблице диаграмму Вейча (рис.6) получим

. (5)

Временные диаграммы, поясняющие работу J-К-триггера, показаны на рис.7.

Чтобы рассмотреть переходные процессы в триггере, необходимо записать функцию перехода J-К-триггера с учетом тактовых сигналов. В зависимости от схемного включения J-К-триггеры описываются одной из функций переходов:

, (6)

. (7)

Функция (7) эквивалентна (6), если на входные сигналы J и К наложить ограничение: эти сигналы не должны применяться при значении тактового сигнала .

При J=К=1 J-К-триггер выполняет функцию асинхронного импульсного Т-тригера (4).

2.5. Счетчики

Подсчет импульсов, выполняемый в устройствах цифровой обработки информации, осуществляется с помощью счетчиков. По назначению счетчики делятся на суммирующие, вычитающие и реверсивные. Суммирующий счетчик увеличивает свое состояние при поступлении на вход очередного импульса. Вычитающий счетчик выполняет счет в обратном направлении, т.е. каждый импульс, поступающий на его вход, уменьшает его состояние на единицу.

Реверсивные счетчики предназначены как для сложения, так и для вычитания в зависимости от управляющих сигналов.

Счетчики в основном строятся на основе триггеров. Основными характеристиками счетчиков являются: модуль счета или коэффициент пересчета счетчика К_сч ; быстродействие счетчика.

Модуль счета характеризует число возможных различных состояний счетчика, т.е. предельное число импульсов, которое может быть сосчитано счетчиком.

Быстродействие счетчика характеризуется: ƒ_сч - частотой поступления счетных импульсов, t_уст – временем установки счетчика.

Простейшим счетчиком является счетный триггер, осуществляющий подсчет импульсов по модулю 2. Соединив последовательно несколько таких триггеров, можно получить схему многоразрядного счетчика с модулем счета К_сч=2ⁿ, где n – число триггеров в счетчике.

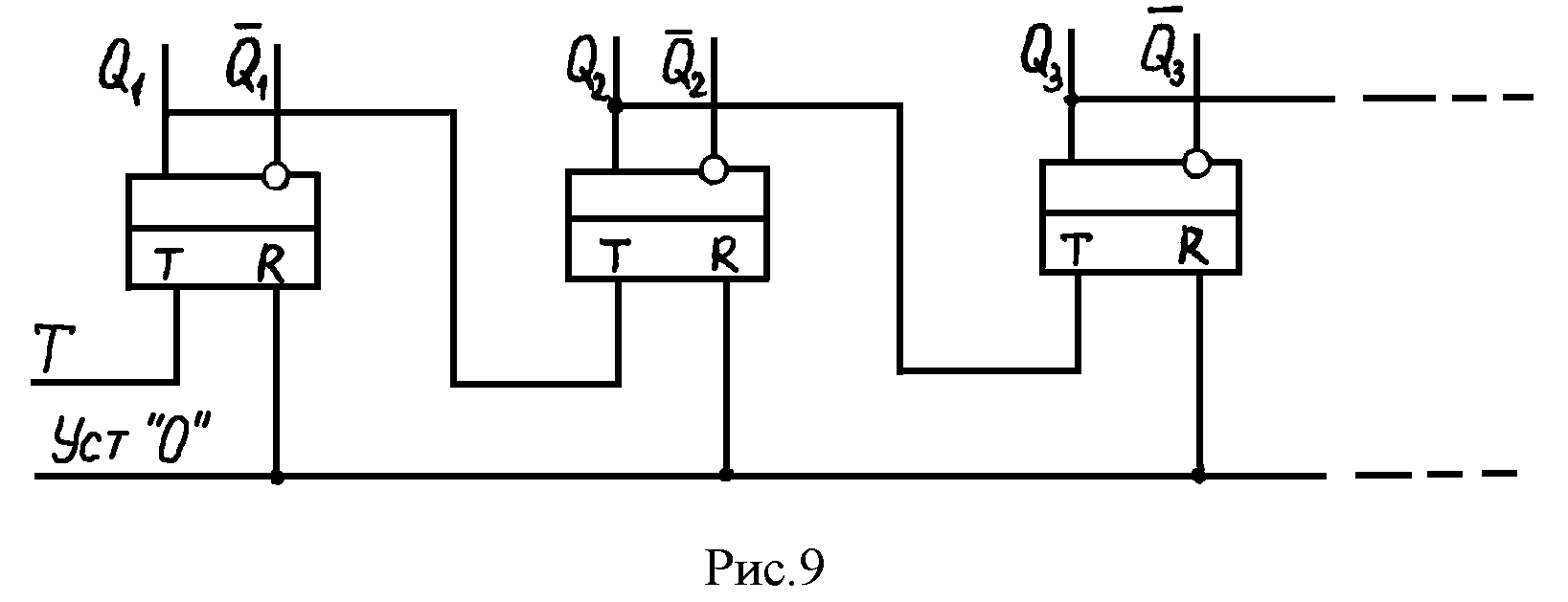Схема счетчика, построенного на Т триггерах, представлена на рис.9.

Счетчик строится таким образом, что выход Q i-го разряда подключен непосредственно к счетному входу следующего i+1-го разряда.

Рассмотрим работу схемы. Пусть счетчики находятся в состоянии (рис.10). При поступлении первого счетного импульса I-й триггер подготовится к переключению и примет состояние Q₁=I по окончании счетного импульса. На счетчике установится код I00. После окончания второго счетного импульса первый триггер возвратится в исходное состояние (Q₁=0), но импульс перехода из «I» в «0» этого триггера вызовет срабатывание 2-го триггера (Q₂=1). В результате после прихода 2-х импульсов в счетчик запишется код 0I0. После 7-го импульса все разряды счетчика будут установлены в единичное состояние. Восьмой импульс вызовет его переполнение, и все разряды установятся в состояние «0».

Наращивая число разрядов счетчика, можно увеличивать его объем К_сч. На рис.10 приведена схема двоичного счетчика на 3 разряда и временные диаграммы, поясняющие принцип работы этой схемы (рис.9).

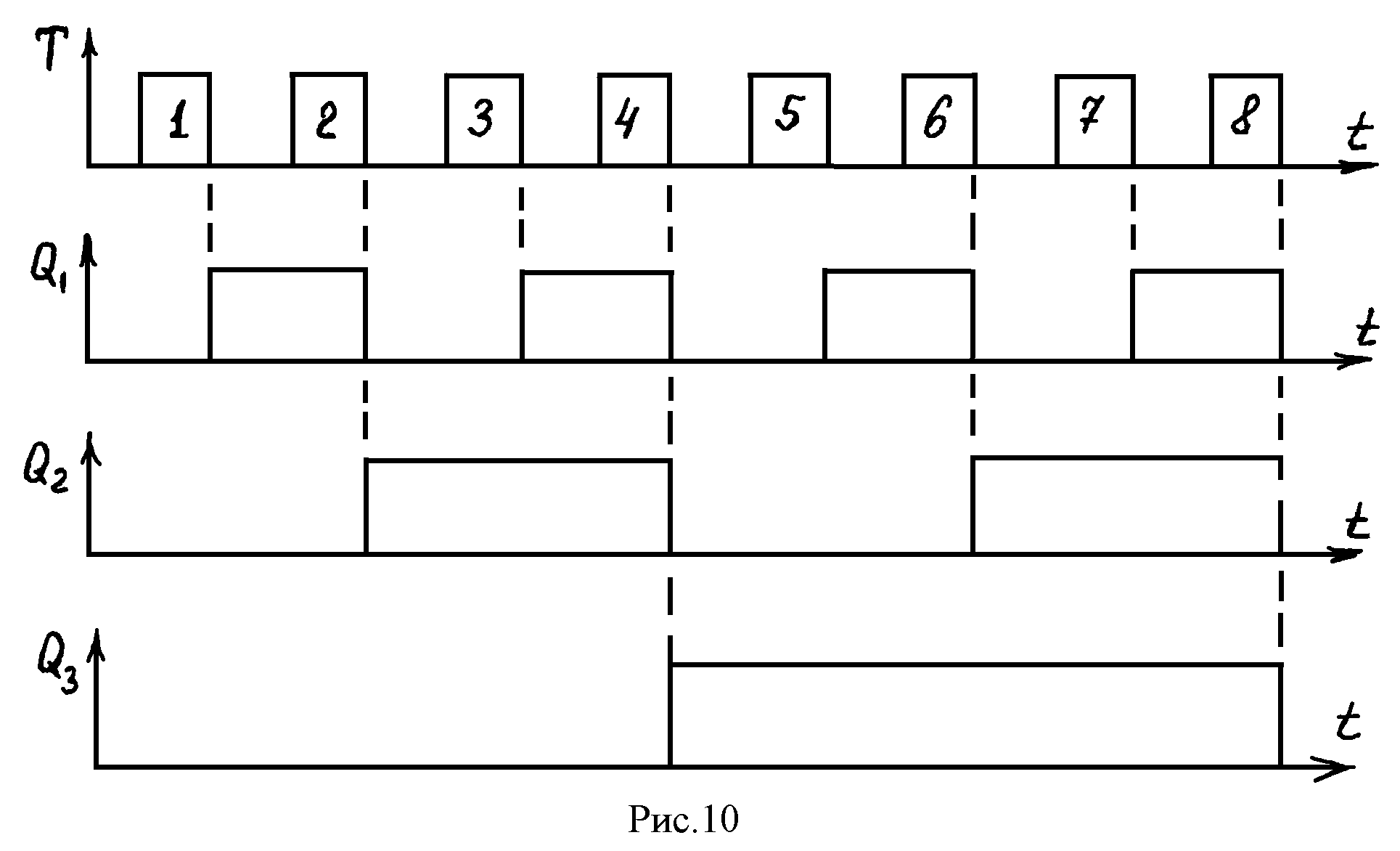
Сигнал Q на выходе последующего триггера имеет в 2 раза меньшую частоту, чем на входе. Следовательно, счетчик может делить частоту сигнала на величину К_сч=2^n.

Счетчики, построенные по указанному принципу, имеют коэффициент деления, кратный двум. На практике возникает необходимость в делении частоты входных сигналов на величину К_сч, не кратную двум. Принцип построения таких счетчиков заключается в исключении лишних, избыточных состояний счетчика. Число триггеров в счетчике выбирается из условия: число триггеров n-счетчика должно быть равно ближайшему целому числу, большему или равному величине log₂К_сч. Исключение избыточных состояний осуществляется, например, возвратом счета в исходное состояние после поступления требуемого числа импульсов (N= К_сч). Например, при реализации делителя на три необходимо использовать два триггера, которые могут осуществлять деление на величину К_сч=4. Значит, имеется одно избыточное состояние (11), которое необходимо исключить. Для исключения избыточного состояния используется декодирующий состояние (01) и разрешающий после этого сброс счетчика входным импульсом в исходное состояние (00).

3. Описание лабораторной установки

Лабораторная установка состоит из макета, включающего в себя:

• генератор одиночных импульсов, запускающийся от кнопки;

• генератор периодической последовательности импульсов;

• набор различных типов интегральных триггеров и счетчик, построенный на их основе.

В макете предусмотрена возможность подачи различных сигналов с помощью перемычек. Состояние схем индицируется светодиодами.

4. Задание на лабораторную работу и порядок ее выполнения

1) Внимательно ознакомьтесь с рекомендованной литературой и устройством макета.

2) Исследуйте работу триггеров от генератора одиночных импульсов и составьте для них таблицы истинности.

3) Соберите счетчик с коэффициентом счета К_сч=8 и изучите его работу от генератора одиночных импульсов.

4) Соберите счетчик с коэффициентом счета, заданным преподавателем и изучите его работу.

5. Содержание отчета о работе

Отчет должен содержать схемы исследуемых элементов и устройств, осциллограммы входных и выходных сигналов, а также таблицы функционирования.

6. Контрольные вопросы.

1) Поясните принцип работы и назначение RS триггера.

2) Поясните принцип работы и назначение D и Т триггеров.

3) Поясните принцип работы У-К-триггера.

4) Каким образом можно построить счетчик импульсов с коэффициентом счета кратным двум на Т, D или У-К-триггерах?

5) Каким образом можно построить счетчик импульсов с коэффициентами счета не кратным двум?

ЛАБОРАТОРНАЯ РАБОТА №5

ПРИМЕНЕНИЕ МУЛЬТИМЕТРА В ИЗМЕРЕНИЯХ