11. Виды дисперсий.

Дисперсия - средний квадрат отклонений индивидуальных значений признака от их средней величины

Различают три вида дисперсий:

• общая;

• средняя внутригрупповая;

• межгрупповая.

• Общая дисперсия ( 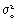) характеризует вариацию признака всей совокупности под влиянием всех тех факторов, которые обусловили данную вариацию. Эта величина определяется по формуле

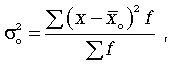
где - общая средняя арифметическая всей исследуемой совокупности.

• Средняя внутригрупповая дисперсия ( ) свидетельствует о случайной вариации, которая может возникнуть под влиянием каких-либо неучтенных факторов и которая не зависит от признака-фактора, положенного в основу группировки. Данная дисперсия рассчитывается следующим образом: сначала рассчитываются дисперсии по отдельным группам (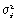 ), затем рассчитывается средняя внутригрупповая дисперсия :

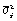где n_i - число единиц в группе

• Межгрупповая дисперсия  (дисперсия групповых средних) характеризует систематическую вариацию, т.е. различия в величине исследуемого признака, возникающие под влиянием признака-фактора, который положен в основу группировки. Эта дисперсия рассчитывается по формуле

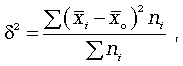
где - средняя величина по отдельной группе.

Все три вида дисперсии связаны между собой: общая дисперсия равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии:

(6.11)

Данное соотношение отражает закон, который называют правилом сложения дисперсий. Согласно этому закону (правилу), общая дисперсия, которая возникает под влиянием всех факторов, равна сумме дисперсий, которые появляются как под влиянием признака-фактора, положенного в основу группировки, так и под влиянием других факторов. Благодаря правилу сложения дисперсий можно определить, какая часть общей дисперсии находится под влиянием признака-фактора, положенного в основу группировки.

Свойства дисперсии.

0. Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.

1. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.

2. Уменьшение или увеличение каждого значения признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в раз, а среднее квадратическое отклонение - в к раз.

3. Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной: . Если А равна нулю, то приходим к следующему равенству: , т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.

Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.

12. Индексный метод

В статистике под индексом понимается относительная величина (показатель), выражающая изменение сложного экономического явления во времени, в пространстве или по сравнению с планом. Индексы используются и для выявления структурных сдвигов в народном хозяйстве.

Индексы рассчитываются как для сложного явления (общие или сводные), так и для отдельных его элементов (индивидуальные индексы). В индексах, характеризующих изменение явления во времени различают базисный и отчетный (текущий) периоды. Базисный период - это период времени к которому относится величина, принятая за базу сравнения. Обозначается он подстрочным знаком "0". Отчетный период - это период времени, к которому относится величина, подвергающаяся сравнению. Обозначается он подстрочным знаком "1".

Индивидуальные индексы - это обычная относительная величина. Например, если цена товара в текущем периоде 30 руб., а в базисном была 25 руб., то индивидуальный индекс будет равен или 120%.

Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления. В зависимости от экономического назначения индивидуальные индексы бывают: физического объема продукции, себестоимости, цен, трудоемкости и т.д.

Индекс физического объема продукции: показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным, или сколько процентов составляет.

Индивидуальный индекс цен: - характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным.

Индивидуальный индекс себестоимости единицы продукции: показывает изменение себестоимости.

Сводный индекс - характеризует изменение всей сложной совокупности в целом, т.е. состоящей из несуммируемых элементов. Следовательно, чтобы рассчитать такой индекс надо преодолеть несуммарность элементов совокупности. Это достигается введением дополнительного показателя (соизмерителя). Сводный индекс состоит из двух элементов: индексируемой величины и веса.

Общие индексы строят для количественных (объемных) и качественных показателей. В зависимости от цели исследования и наличия исходных данных используют различные формы построения общих индексов: агрегатная или средневзвешенная.

13. Агрегатный индекс – сложный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Особенность этой формы индекса состоит в том, что непосредственно сравниваются две суммы одноименных показателей.

Индексируемая величина – признак, изменение которого изучается (цена товаров, курс акций, затраты рабочего времени и т.д.). Вес индекса – это величина, служащая для целей соизмерения индексируемых величин.

При выборе веса индекса следует руководствоваться правилом: если строится индекс количественного показателя, то веса берутся за базисный период, при построении индекса качественного показателя используются веса отчетного периода.

Индекс стоимости продукции (товарооборота) ( ) - представляет собой отношение стоимости продукции текущего периода к стоимости продукции в базисном периоде. Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на цену (p).

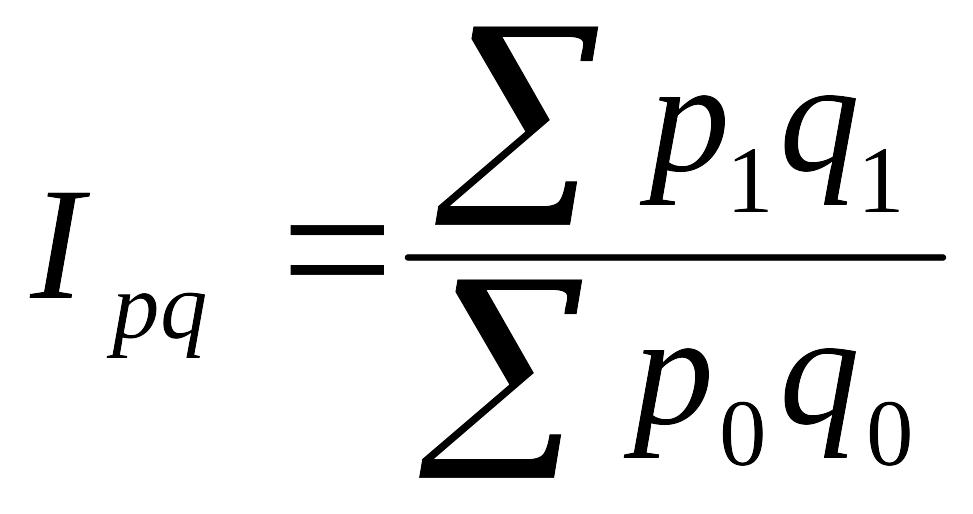
Показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным, или сколько процентов составляет.

Индекс физического объема продукции – это индекс количественного показателя. Индексируемой величиной будет количество продукции, а весом – цена.

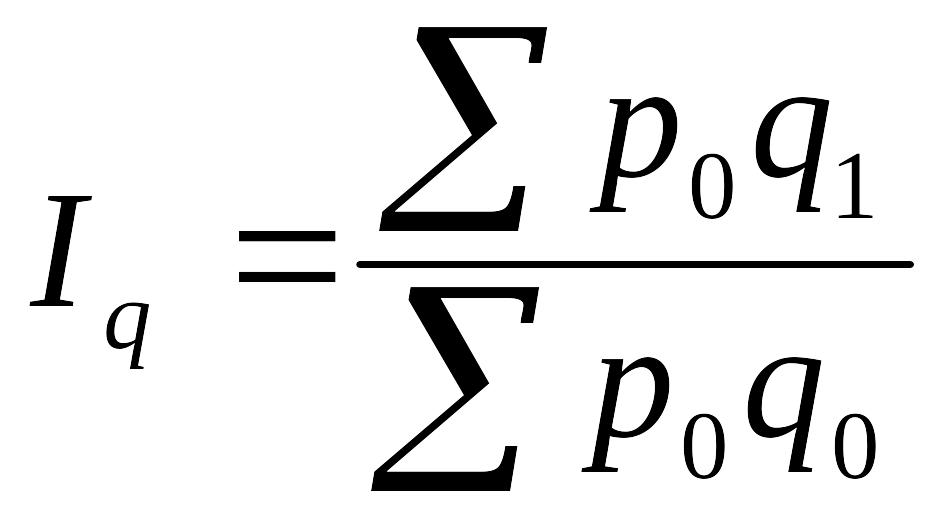
показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения объемов ее производства.

Разность числителя и знаменателя ( ) показывает, на сколько рублей изменилась стоимость продукции в результате изменения объема.

Индекс цен – это индекс качественного показателя. Индексируемой величиной будет цена товара, т.к. этот индекс характеризует изменение цен. Весом будет выступать количество произведенного товаров.

,

в числителе – фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров ценах базисного периода. Показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен. Разность числителя и знаменателя – на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен.

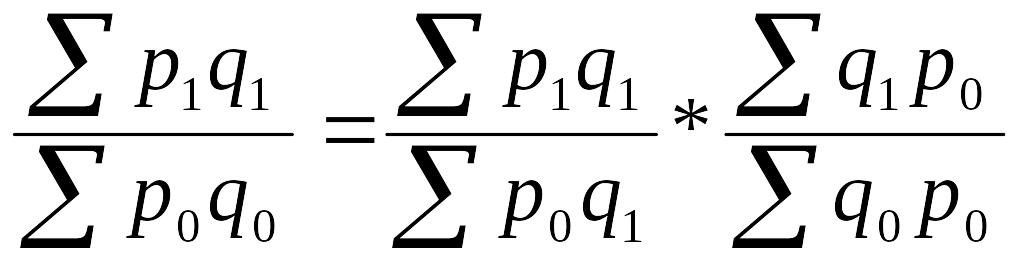Стоимость продукции можно представить как произведение количества товара на его цену. Точно такая же связь существует и между индексами стоимости, физического объема и цен, т.е. , или . Разность числителя и знаменателя каждого индекса-сомножителя выражает размер изменения общей абсолютной величины под влиянием изменения одного фактора.

Методика построения агрегатного индекса предусматривает решение трех вопросов:

1. Какая величина будет индексируемой

2. По какому составу разнородных элементов явления необходимо исчислить индекс

3. Что будет служить весом при расчете индекса.