- •1.Установившееся движение жидкости в напорных трубопроводах. Предварительные замечания. Расчётные зависимости.
- •2.Сложение потерь напора. Полный коэффициент сопротивления.
- •3.Понятия длинных и коротких трубопроводов. Простой трубопровод постоянного диаметра(случай истечения в атмосферу).
- •4.Простой трубопровод. Случай истечения жидкости под уровень. Окончательные расчётные зависимости.
- •5.Особые случаи простого трубопровода(сифон).
- •6.Расчёт всасывающей трубы насоса.
- •7.Простой длинный трубопровод. Истечение под уровень и в атмосферу.
- •8.Последовательное и параллельное соединение труб.
- •9.Потери напора в случае расхода переменного по длине трубы.
- •10.Сложные трубопроводы. Расчёт тупикового трубопровода(случай 10).
- •11.Расчёт замкнутой кольцевой сети.
- •13.Расчётные зависимости для величины гидравлического удара и скорости его распространения.
- •14.Прямой(начальный) и отражённый гидравлические удары.
- •15.Случай постепенного закрытия крана. Полный и неполный гидравлические удары.
- •16.Истечение жидкости из малого отверстия в тонкой стенке при постоянном напоре в атмосферу.
- •17.Типы сжатия струи. Коэффициенты φ, ξ ε,μ для малого отверстия при истечении в атмосферу, инверсия струи. Траектория струи.
- •18.Истечение из малого отверстия под уровень. Понятие малого и большого отверстий.
- •19.Типы насадков. Общая картина движения жидкости при истечении в атмосферу из насадков Вентури.
- •20.Истечение из внешнего круглоцилиндрического насадка в атмосферу. Расчетные зависимости для q и v2. Численные значения коэффициентов ε,ζ,φ, μн.
- •21.Сопоставление истечения жидкости через отверстие в тонкой стенке с истечением через насадок Вентури. Величина вакуума. Работа короткой трубы.
- •22.Истечение в атмосферу или под постоянный уровень жидкости при переменном напоре.
- •23.Истечение газов из отверстий.
- •24.Относительное движение тела и жидкости. Общие сведения.
- •25.Сопротивление давления при обтекании жидкостью твердого тела.
- •26.Критическая глубина русла, нормальная глубина, критический уклон; спокойное, бурное и критическое состояние потока.
- •27.Давление ветра на здание и сооружение.
- •28.Сопротивление трение. Пограничный слой.
- •29.Сопротивление пластинки в потоке при продольном ее обтекании при турбулентном режиме.
- •30.Неравномерное безнапорное установившееся движение воды в каналах. Предварительные указания.
- •31.Гидравлические элементы живого сечения потока в канале.
- •32.Гидравлически наивыгоднейший поперечный профиль трапециидального канала.
- •33.Основные задачи при расчете трапециидальных каналов на равномерное движение воды.
- •34.Ограничение скорости движения воды при расчёте каналов.
- •35.Основные указания о моделировании гидравлических явлений.
- •36.Понятия о подобии гидравлических явлений.
- •37.Основы теории физического моделирования гидравлических явлений. Общие указания.
- •38. Критерии динамического подобия.
- •39.Удельная энергия сечения русла.
- •40.Нормальная глубина, критический уклон.
13.Расчётные зависимости для величины гидравлического удара и скорости его распространения.
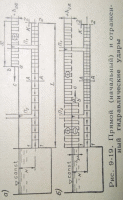
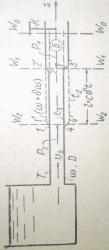
Представим на рисунке цилиндрический трубопровод Т, на в конце которого имеется частично открытый кран К. Будем считать, что в трубопроводе сечении W0—W0, намеченном у крана, скорость движения жидкости = v0. Представим себе далее, что в момент времени t=0 открытие крана К мгновенно изменилось, в связи с чем скорость в сечении W0—W0 мгновенно изменилась (например, уменьшилась) на величину δv, у крана зародилась область возмущения Б. Будем считать, что в некоторый момент времени t1 граница области возмущения занимает положение W1—W1. в некоторый момент t2 = t1 + δt эта граница переместится в положение W2—W2 Расстояние между вертикалями. W1—W1 и W2—W2 равно l=c*δt, за время δt стенки трубы на длине l раздадутся и примут положение, показанное на чертеже штриховой линией.
Применив
к отсеку жидкости W1—W2,
заключенному
между сечениями W1—W1
и
W2—W2
уравнение
неразрывности и теорему
количества движения, получаем следующие
расчетные зависимости:а) Зависимость
для величины hуд:
hуд=(руд/ϒ)=-(с/g)*δv,
где δv-
положительное
или отрицательное приращение (во
времени) скорости движения жидкости.
Именно таким образом выражается величина
гидравлического удара. Как видно, при
положительном δv,
т.е. при увеличении начальной скорости
v0,
получаем отрицательное значение hуд,
обусловливающее возникновение волны
понижения давления. В случае полного
закрытия крана, когда δv=-
v0,
величина гидравлического удара
оказывается равной: :
hуд=(с/g)*v0.
б)Зависимость
для
величины с (в случае круглой
трубы):с-скорость распространения
ударной волны,
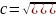
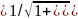 где
Еж
— модуль объемной упругости жидкости;
Ет
—
модуль упругости материала стенок
трубы; D
—
внутренний диаметр трубы; е
—
толщина стенок трубы. Введем обозначения
где
Еж
— модуль объемной упругости жидкости;
Ет
—
модуль упругости материала стенок
трубы; D
—
внутренний диаметр трубы; е
—
толщина стенок трубы. Введем обозначения
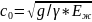 -
скорость распространенна звука в
покоящейся жидкости, для воды с
0
=
1425 м/сек.
-
скорость распространенна звука в
покоящейся жидкости, для воды с
0
=
1425 м/сек.
(9-55)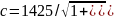 ,м/сек, как видно,
,м/сек, как видно,
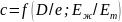 .
Надо
заметить, что
величина с
может
измеряться сотнями и даже тысячами
метров в секунду.
.
Надо
заметить, что
величина с
может
измеряться сотнями и даже тысячами
метров в секунду.
14.Прямой(начальный) и отражённый гидравлические удары.
Представление
о гидравлическом ударе будет неполным,
если мы не учтем еще следующего
существенного обстоятельства. Представим
трубу,
заполненную жидкостью; один конец трубы
открыт (сечение 1-1), другой конец
прикрывается краном К
(сечение
2—2).
Как
уже известно, в случае мгновенного
закрытия крана в жидкости зарождается
волна положительного давления, имеющая
вертикальный «лоб» ab,
причем
эта волна движется вдоль трубы. Как
только «лоб» указанной положительной
волны доходит до открытого конца трубы
(в
сечении
1—1)
возникает
отраженная
отрицательная
волна,
представляющая
собой зеркальное отображение прямой
волны,
повернутое
на 180°. «Лоб» а'Ь'
отраженной
отрицательной
волны движется
с той
же скоростью с
в
сторону,
противоположную
положительной
волне, положительные
давления
прямой (начальной)
волны и
отрицательные давления
отраженной волны
складываются; в результате на участке
трубы охваченном
в данный момент
времени отраженной волной, давление,
обусловленное
гидравлическим ударом
оказывается =0. Как
только «лоб» указанной отрицательной
волны доходит
до закрытого конца
трубы, в этом месте (в Сечении 2—2)
возникает
отраженная отрицательная волна, со
скоростью с
в
сторону, противоположную той отрицательной
волне, которая подошла к сечению 2—2.
У
открытого конца трубы 1—1
всегда
зарождаются отраженные волны обратного
знака (по отношению к прямым волнам,
подошедшим к этому концу); у закрытого
же конца трубы 2—2
всегда
зарождаются отраженные волны того же
знака, что и прямые волны,
подошедшие
к этому
концу.
Обозначим
через t0
время пробега «лба» волны аЬ
от
сечения 2—2
до сечения 1-1: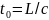 ,где
L
—
длина трубы. Пользуясь этим обозначением
укажем следующее:а) в момент
,где
L
—
длина трубы. Пользуясь этим обозначением
укажем следующее:а) в момент
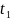 = t0
времени,
отсчитываемого от момента закрытия
крана, по всей длине трубы давление
должно быть одинаковым и =
hуд.
б)
в момент времени
= t0
времени,
отсчитываемого от момента закрытия
крана, по всей длине трубы давление
должно быть одинаковым и =
hуд.
б)
в момент времени
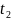 = 2t0
давление
по всей длине трубы должно быть равным
нулю. в) в момент времени
= 2t0
давление
по всей длине трубы должно быть равным
нулю. в) в момент времени
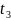 = 3t0
давление
по всей длине трубы должно быть равным
-hуд.
г)
в момент времени t4
= 4t0
давление по всей длине трубы должно
быть равным нулю. Таким образом, полный
период tn
колебания
давления в любом неподвижном поперечном
сечении трубы будет равен четырехкратному
времени пробега «лбом» волны расстояния
L:
= 3t0
давление
по всей длине трубы должно быть равным
-hуд.
г)
в момент времени t4
= 4t0
давление по всей длине трубы должно
быть равным нулю. Таким образом, полный
период tn
колебания
давления в любом неподвижном поперечном
сечении трубы будет равен четырехкратному
времени пробега «лбом» волны расстояния
L:
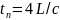 . Если
наметим на трубе неподвижное сечение
А-А,
то
давление в этом сечении будет изменяться
во времени. В реальных условиях указанное
колебание величины давления должно
постепенно затухать.
. Если
наметим на трубе неподвижное сечение
А-А,
то
давление в этом сечении будет изменяться
во времени. В реальных условиях указанное
колебание величины давления должно
постепенно затухать.