- •1.Установившееся движение жидкости в напорных трубопроводах. Предварительные замечания. Расчётные зависимости.
- •2.Сложение потерь напора. Полный коэффициент сопротивления.
- •3.Понятия длинных и коротких трубопроводов. Простой трубопровод постоянного диаметра(случай истечения в атмосферу).
- •4.Простой трубопровод. Случай истечения жидкости под уровень. Окончательные расчётные зависимости.
- •5.Особые случаи простого трубопровода(сифон).
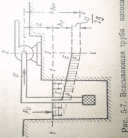
- •6.Расчёт всасывающей трубы насоса.
- •7.Простой длинный трубопровод. Истечение под уровень и в атмосферу.
- •8.Последовательное и параллельное соединение труб.
- •9.Потери напора в случае расхода переменного по длине трубы.
- •10.Сложные трубопроводы. Расчёт тупикового трубопровода(случай 10).
- •11.Расчёт замкнутой кольцевой сети.
- •13.Расчётные зависимости для величины гидравлического удара и скорости его распространения.
- •14.Прямой(начальный) и отражённый гидравлические удары.
- •15.Случай постепенного закрытия крана. Полный и неполный гидравлические удары.
- •16.Истечение жидкости из малого отверстия в тонкой стенке при постоянном напоре в атмосферу.
- •17.Типы сжатия струи. Коэффициенты φ, ξ ε,μ для малого отверстия при истечении в атмосферу, инверсия струи. Траектория струи.
- •18.Истечение из малого отверстия под уровень. Понятие малого и большого отверстий.
- •19.Типы насадков. Общая картина движения жидкости при истечении в атмосферу из насадков Вентури.
- •20.Истечение из внешнего круглоцилиндрического насадка в атмосферу. Расчетные зависимости для q и v2. Численные значения коэффициентов ε,ζ,φ, μн.
- •21.Сопоставление истечения жидкости через отверстие в тонкой стенке с истечением через насадок Вентури. Величина вакуума. Работа короткой трубы.
- •22.Истечение в атмосферу или под постоянный уровень жидкости при переменном напоре.
- •23.Истечение газов из отверстий.
- •24.Относительное движение тела и жидкости. Общие сведения.
- •25.Сопротивление давления при обтекании жидкостью твердого тела.
- •26.Критическая глубина русла, нормальная глубина, критический уклон; спокойное, бурное и критическое состояние потока.
- •27.Давление ветра на здание и сооружение.
- •28.Сопротивление трение. Пограничный слой.
- •29.Сопротивление пластинки в потоке при продольном ее обтекании при турбулентном режиме.
- •30.Неравномерное безнапорное установившееся движение воды в каналах. Предварительные указания.
- •31.Гидравлические элементы живого сечения потока в канале.
- •32.Гидравлически наивыгоднейший поперечный профиль трапециидального канала.
- •33.Основные задачи при расчете трапециидальных каналов на равномерное движение воды.
- •34.Ограничение скорости движения воды при расчёте каналов.
- •35.Основные указания о моделировании гидравлических явлений.
- •36.Понятия о подобии гидравлических явлений.
- •37.Основы теории физического моделирования гидравлических явлений. Общие указания.
- •38. Критерии динамического подобия.
- •39.Удельная энергия сечения русла.
- •40.Нормальная глубина, критический уклон.
5.Особые случаи простого трубопровода(сифон).
Сифон.
Сифоном называется самотечная труба,
часть которой расположена выше горизонта
жидкости в сосуде, который её питает.
Рассмотрим истечение жидкости из сифона
под уровень. Наметим сечение трубы n-n
и обозначим превышение его над горизонтом
жидкости: в левом сосуде- через h’
и в правом сосуде- через h”.
Если предположить, что жидкость,
заполняющая сифон, находится в покое,
то можно написать: а) давление в сечении
n-n
с левой стороны р1=ра+(-ϒ
h’);б)р2=ра+(-ϒ
h”),
где (-h’)
и(- h”)-
соответствующие заглубления сечения
n-n
под горизонтом жидкости в сосудах. Из
рисунка видно, что жидкость не может
находится в покое, р1>p2,
она будет двигаться в сторону меньшего
давления. Рассмотрим установившееся
движение жидкости в сифоне (Z=const).
Наметим 2 сечения 1-1 и 3-3. Соединяя эти
сечения ур-нием Бернулли получим
формулу для расхода в виде: Q=μTω
,
где μТ=
=
.
Характерным для сифона является то,
что в нём имеет место вакуум. Наибольшая
величина вакуума будет в сечении,
наиболее высоко расположенном. Найдём
максимальную величину вакуума (hвак)макс
в сифоне. С этой целью наметим по линии
n-n,
где ищем вакуум, сечение 2-2 и затем
соединим сечения 1-1 и 2-2 ур-нием Бернулли
(плоскость сравнения проведём на уровне
горизонта жидкости в левом сосуде):
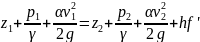 ,
где z1=0,
z2=h’,
р1/ϒ=ра/ϒ;
р2/ϒ=рn/ϒ,
,
где z1=0,
z2=h’,
р1/ϒ=ра/ϒ;
р2/ϒ=рn/ϒ,
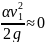 ,
, ,
здесь v-
скорость в трубе, рп-
давление в сечении n-n.Потери
напора hf’
по пути от сечения 1-1 до сечения 2-2
выражаем обычной зависимостью hf’=
ζf’(v2/2g),где
ζf’-
полный коэф. сопротивления, учитывающий
потерю напора не во всей трубе, а только
от сеч.1-1 до сеч.2-2. Т.о. получаем:
(pa/ϒ)=h’+(pn/ϒ)+(v2/2g)+
ζf’(v2/2g)
или (pa/ϒ)
-(pn/ϒ)=h’+(1+
ζf’)(v2/2g).
Т.к. (pa/ϒ)
-(pn/ϒ)=
(hвак)макс,
то (hвак)макс=
h’+(1+
ζf’)(v2/2g).
Напорная линия Е-Е и пьезометрическая
линия Р-Р в случае сифона показаны на
рисунке.
,
здесь v-
скорость в трубе, рп-
давление в сечении n-n.Потери
напора hf’
по пути от сечения 1-1 до сечения 2-2
выражаем обычной зависимостью hf’=
ζf’(v2/2g),где
ζf’-
полный коэф. сопротивления, учитывающий
потерю напора не во всей трубе, а только
от сеч.1-1 до сеч.2-2. Т.о. получаем:
(pa/ϒ)=h’+(pn/ϒ)+(v2/2g)+
ζf’(v2/2g)
или (pa/ϒ)
-(pn/ϒ)=h’+(1+
ζf’)(v2/2g).
Т.к. (pa/ϒ)
-(pn/ϒ)=
(hвак)макс,
то (hвак)макс=
h’+(1+
ζf’)(v2/2g).
Напорная линия Е-Е и пьезометрическая
линия Р-Р в случае сифона показаны на
рисунке.

6.Расчёт всасывающей трубы насоса.
Всасывающей трубой насоса называется труба, по которой насос засасывает жидкость из бассейна. Эта труба обычно так же, как и сифон, характеризуется наличием вакуума. Наибольшая величина вакуума будет непосредственно у насоса, перед его рабочим колесом (сеч.2-2)
Всасывающей трубой
насоса называется труба, по которой
насос засасывает жидкость из бассейна.
Эта труба обычно так же, как и сифон,
характеризуется наличием вакуума.
Наибольшая величина вакуума будет
непосредственно у насоса, перед его
рабочим колесом (сеч.2-2). Такой вакуум
можно найти, соединяя уравнением
Бернулли сечение 1-1, намеченное по
поверхности жидкости в бассейне, и
сечение 2-2.
Его можно
также определить подставив в формулу
(hвак)макс=
h’+(1+
ζf’)(v2/2g)
вместо h'
величину а,
означающую
превышение оси насоса над горизонтом
жидкости в бассейне, и вместо ζf’
величину ζf,
т. е. полный
коэффициент сопротивления, учитывающий
потери напора во всей трубе. При этом
получаем:
(hвак)макс=a+(1+
ζf)(v2/2g),
(hвак)макс-вакуум
перед рабочим колесом насоса. Различные
типы насосов допускают различную
величину вакуума. Обычно вакуум перед
рабочим колесом насоса должен
удовлетворять условию:
(hвак)нас м вод.ст.
Величина допустимого
вакуума зависит не только от типа
насоса, но и от температуры и рода
жидкости. С увеличением температуры
жидкости величина допустимого
вакуума снижается. Зная допустимый
вакуум для данного насоса и данной
жидкости (hвак)доп
можно по формуле найти предельное
максимальное возвышение над горизонтом
жидкости в бассейне:адоп=(hвак)доп-(1++
ζf)(v2/2g).
В случае горячей воды адоп
может быть отрицательным; в этом случае
насос приходится располагать ниже
горизонта воды в колодце.
м вод.ст.
Величина допустимого
вакуума зависит не только от типа
насоса, но и от температуры и рода
жидкости. С увеличением температуры
жидкости величина допустимого
вакуума снижается. Зная допустимый
вакуум для данного насоса и данной
жидкости (hвак)доп
можно по формуле найти предельное
максимальное возвышение над горизонтом
жидкости в бассейне:адоп=(hвак)доп-(1++
ζf)(v2/2g).
В случае горячей воды адоп
может быть отрицательным; в этом случае
насос приходится располагать ниже
горизонта воды в колодце.