34.Ограничение скорости движения воды при расчёте каналов.

Средняя скорость движения воды в проектируемом канале должна лежать в пределах

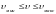
,где vмакс – максимальная допустимая средняя скорость при равномерном движении воды или максимальная неразмывающая скорость; считают, что при v>vмакс русло канала будет размываться водой; vмин – минимальная допустимая средняя скорость при равномерном движении воды(минимальная незаиляющая скорость );считают, что при v<vмин русло канала будет заиливаться отлагающимися в нём наносами, которые несёт поток.

Действительная скорость зависит от уклона канала. Макс.скорость не зависит от уклона, но должна зависеть от рода материала, из которого выполнены стенки, образующие канал, и в некоторых случаях от глубины воды в канале. Что касается мин.доп.скоростей, то численные значения их м/б установлены,напр-р, по Техн.условиям и нормам, согласно которым

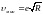
Где е – к-т, учитывающий кол-во взвешенных наносов, их гранулометрический состав и шероховатость русла. 1.мероприятия по увеличению скорости vмакс .Здесь приходится применять,напр-р, покрытие откосов и дна канала каким-либо креплением в виде каменной момтовой, бетонной облицовки и т.п. 2.мероприятия по уменьшению скорости vмин .

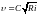
Как видно, что бы уменьшить скорость, необх-мо уменьшить или R, или С, или i.В соответствии с этим следует различать три разных приёма:а)изменение формы поперечного сечения канала, что бы несколько уменьшить гидр.радиус , но за счёт только этого не возможно значительно уменьшить скорость;б)создание т.н. искуственной шероховатости, в рез-те чего повышается численное значение к-та шероховатости n и снижается численное значение к-та Шези.Этот приём м/б неприемлем с экономической т.з.;в)уменьшение уклона дна канала.обычно приходится обращаться именно к этому приёму, при этом по длине канала устраивают перепады.

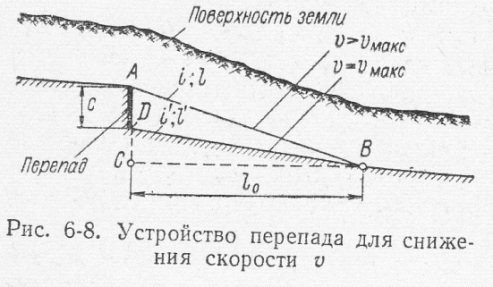
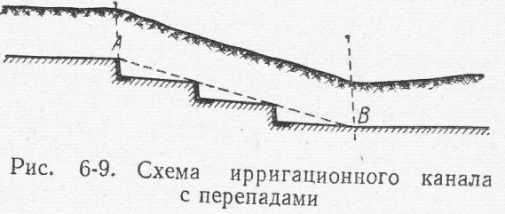
Стремясь получить миним. объём земляных работ, линию дна АВ канала назначают примерно параллельной пов-ти земли. Т.о., уклон дна канала на первом этапе расчёта принимается равным уклону пов-ти зели.Если, приняв этот уклон и выполнив гидр.расчёт, получим скорость больше макс.допустимой, то в этом случае следует устроить в канале перепад АD и уменьшить уклон i до i’, где i’ опред-т из условия v=v_макс . Легко видеть, что такое решение будет, с одной стороны, технически приемлемо, с др.же стороны, экономически наиболее выгодно. Из чертежа видно, что высота перепада с будет равна: с=АС-АD=il-i’l’, где l и l’-длины канала. Т.к. уклоны i каналов вообще малы, то можно считать, что l≈l’≈l_o , где l_o –длина гориз.проекции канала. Учитывая это можем написать, что с=(i-i’) l_o . Если величина с получается большой(более 2-3 м), то по длине канала устраивают несколько перепадов, разбив общее падение на отдельные части. Сами перепады устраивают в виде подпорных стен и т.п.

35.Основные указания о моделировании гидравлических явлений.

Положим, что мы приняли некоторый определённый масштаб длин: a_l=l_м:l_н . Будем считать, что на жидкость действуют две системы сил: силы тяжести и силы трения. Как было отмечено, для достижения динамического подобия необходимо, помимо кинематического подобия, одновременно выдержать два требования. Каждое из них приводит нас к следующему: 1-ое требование.Здесь необходимо соблюсти равенство 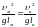. Заметим, что ускорение силы тяжести g в случае модели и натуры одинаково. Ниже пользуемся критериями подобия, выраженными через среднюю скорость: 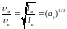. Такому условию для сходственных живых сечений должны удовлетворять скорости в натуре и на модели, если соблюдено равенство чисел Фруда. Расходы Qм и Qн должны здесь удовлетворять условию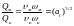 . Масштаб времени получаем след.образом:

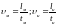, деля , откуда .

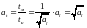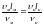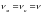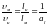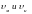2-ое требование.Здесь необходимо соблюсти равенство , считая , т.е. предполагая, что в лаборатории исп-ся та же жидкость, что и в натуре. Далее получаем, что . Такому условию должны удовлетворять скорости , если соблюдено равенство чисел Рейнольдса. Расходы Qм и Qн должны здесь удовлетворять условию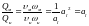

Выполняя эксперименты,необходимо учитывать след.обст-ва:1) можно показать, что бурное безнапорное движение получается, если число Фруда больше единицы, если же оно меньше единицы – получим спокойное движение.Моделируя спокойное движение, в кач-ве «исходного» граничного сечения следует принять намеченное в конце моделируемого участка русла.В случае бурного – в начале. 2)если в натуре имеем турб.движение, то в условиях модели должны иметь такое же движение;поэтому в этом случае возникает доп.условие (Re)м>(R ek)м , где (R ek)м - критическое число для модели. Если в натуре имеем турб.движение, отвечающее квадратичной области сопротивления, то необходимо требовать условия: (Re)м≥(R e’пред)м .3) вопросы моделирования потока также значительно усложняются при учёте размыва русла и движения наносов, аэрации потока, образования вакуума в потоке.