22.Истечение в атмосферу или под постоянный уровень жидкости при переменном напоре.

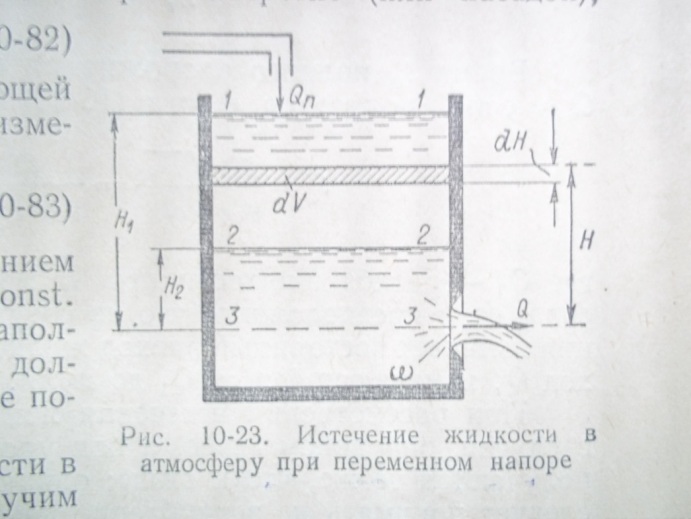
Представим на рис.: сосуд, наполненный жидкостью до уровня 1-1. Введем обозначения:Ω — площадь горизонтального сечения сосуда; в общем случае, когда сосуд нецилиндрический, Ω=f₁(Н). Q- расход жидкости, вытекающей через отверстие, Q=μω . Q_П- расход жидкости, поступающей в сосуд; вообще расход Q_n может изменяться с течением времени t: Q_П=f(t). Если Q_П > Q, то сосуд будет наполняться и уровень жидкости в нём должен подниматься до тех пор, пока не получим равенство Q_n = Q. Если Qn < Q, то уровень жидкости в сосуде будет опускаться, пока не получим такое Н, при котором Q_n =Q. Рассмотрим случай, когда Q_n < Q, и найдем время t, в течение которого горизонт жидкости 1—1 опустится до положения 2-2. При решении этой задачи рассуждаем следующим образом. За бесконечно малый отрезок времени dt из сосуда вытекает объем жидкости 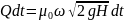. За этот же отрезок времени в сосуд поступает объем жидкости Q_Пdt. Изменение объема жидкости в сосуде (dV) можно представить двумя разными зависимостями: с одной стороны, . С другой же стороны: dV= ΩdH, где объём ΩdH показан на чертеже штриховкой. Приравнивая правые части и проинтегрировав в пределах Н₁ и Н₂,получим для цилиндрического сосуда и Q_П=0 :

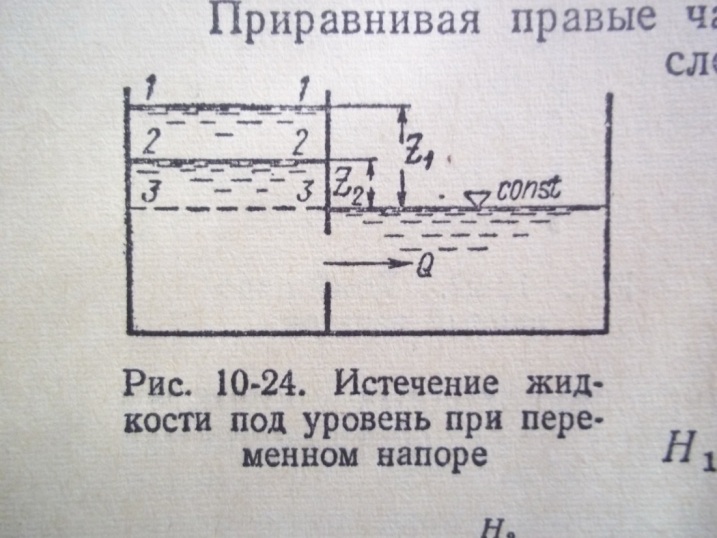
если Ω≠ const, то уравнение решается методом конечных разностей. При истечении жид-ти не в атмосферу, а под уровень расчётные формулы получаются такие же, а величину Н следует понимать не как заглубление центра тяжести отверстия под уровень жидкости в сосуде, а как разность уровней z жидкости с сосудах.

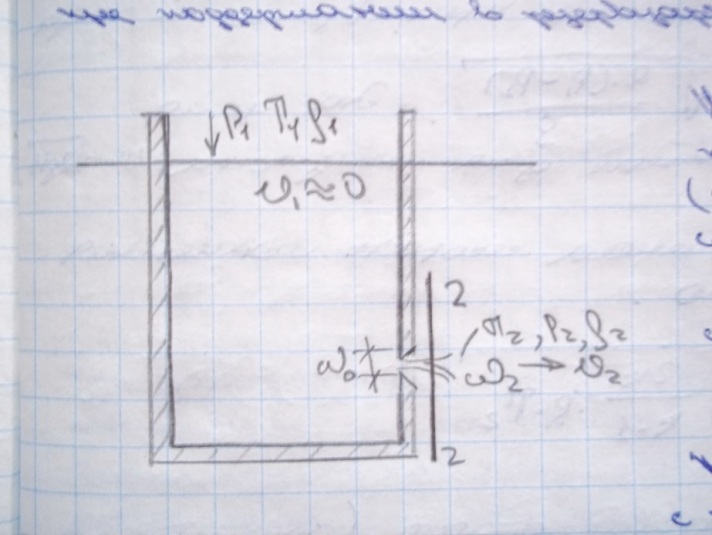
23.Истечение газов из отверстий.

Рассмотрим истечение газа из резервуара через небольшое отверстие при поддержании в резервуаре постоянного давления. Рассмотрим следующую схему:Пусть внутри сосуда р₁; плотность ρ₁; температура Т₁ (сечение 1-1), а на выходе в сечение 2-2 соответственно р₂, ρ₂, Т₂. Будем считать скорость на входе υ₁=0, а на выходе υ₂. Процесс истечение газа с термодинамической точки можно считать адиабатическим т.к. на весьма коротком пути от резервуара до сечения 2-2 влияние теплообмена между выходящим газом и внешним пространством можно пренебречь. Запишем уравнение Бернулли при адиабатическом процессе для сечений 1-1 и 2-2 временно пренебрегая потерями энергииz₁+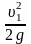 = z₂+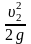 - 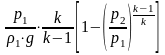, где k – адиабатическая постоянная газа. k= , где С_р –теплоемкость газа при постоянном давлении. 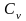- теплоемкость газа при постоянном объеме. Т.о. этим показателем учитывается сжимаемость газа. Е₀=k*p. Пренебрегая геометрическими высотами и скоростью подхода уравнение Бернулли примет вид: 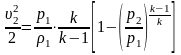, выразим отсюда скорость 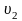: . Это выражение носит название ур-ния Сен-Венана для скорости истечения газа. Преобразовав это выражения можно найти значения выражений р₁ и р₂: 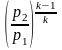=1- , р₂= р₁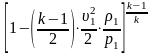 имеем в ввиду что отношение k*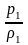 =C₁², где C₁² – скорость распространения звука в покоящемся газе. Можно получить выражение скорости вытекания газа из сосуда: =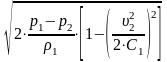 , во всех случаях когда отношение значительно меньше 1 т.е. при , то этим отношением можно пренебречь и тогда скорость истечения равна: =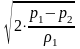 т.е. та же формула что и для капельной жидкости (υ= 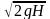). Максимально возможная скорость истечения газа будет при р₂=0: 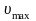= 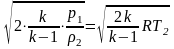. Массовый расход вытекающего газа(пренебрегая сжатием струи) равен: М= , где ω – площадь сечения отверстия. Влияние сжатия струи на подходе к отверстию и др. неучтенных факторов учитывается как и при истечении несжимаемой жидкости введением коэффициента μ т.е. М= .