1.Установившееся движение жидкости в напорных трубопроводах. Предварительные замечания. Расчётные зависимости.

Рассмотрим установившееся равномерное напорное турбулентное движение любой жидкости в круглых цилиндрических неподвижных трубах. Внутренний диаметр труб обозначаем через D, длину их через L. Гидравлические элементы живого сечения рассматриваемого потока: ω=πD²/4; χ=πD; R=ω/χ=D/4. главнейшие уравнения, которыми пользуемся: уравнение неразрывности; уравнение Бернулли; уравнение для определения потерь напора. Рассматриваем случаи отвечающие квадратичной области сопротивления. что касается трубопроводов, относящихся к доквадратичной области сопротивления и области гладких труб, то их расчёт отличается только тем, что при определении потерь напора вместо формулы Шези используется формула Вейсбаха-Дарси.При расчёте трубопроводов следует различать 2 случая.1)когда местные потери напора отсутствуют или когда этими потерями можно пренебречь ввиду их малости в сравнении с потерями по длине. В этом случае имеем только потери напора h_L, причём выражаем их через модуль расхода К: h_L=(Q²/K²)*L, где Q²/K²=J. Для круглой трубы К²=ω²С²R=( πD²/4)²С²(D/4)=(π²С²/64)D⁵,где С=f(n,R) и для квадратичной области сопротивления С=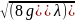 . Модуль расхода является функцией шероховатости и диаметра трубы.2) когда имеются местные потери напора Ʃh_j причём ими нельзя пренебречь сравнительно с величиной h_L. здесь величину h_Lудобно выражать через скоростной напор согласно зависимости Вейсбаха-Дарси: h_L=λ(L/D)(v²/2g). Под длиной L понимают длину всей трубы, предполагая, что длины участков с местными потерями напора пренебрежимо малы. Местные потери определяются по зависимости Вейсбаха: h_j=ζ_j(v²/2g).

2.Сложение потерь напора. Полный коэффициент сопротивления.

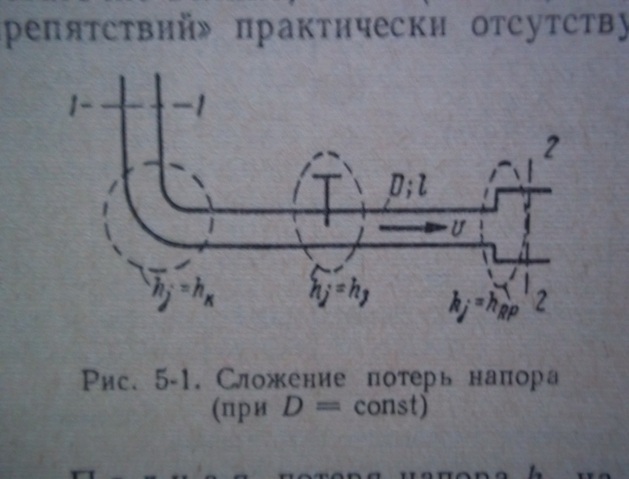
Рассмотри некоторый трубопровод, имеющий по своей длине различные местные препятствия, расстояние между которыми достаточно велико. Рисунок.

Полная потеря напора h_f на пути от сечения 1-1 до сечения 2-2 выразится в виде: h_f=h_L+ Ʃh_j. Рассмотрим отдельно каждое слагаемое этого выражения.1) сумма местных потерь напора Ʃh_j. Из рисунка видно, что Ʃh_j=h_к+h_з+h_р.р, где h_к–местная потеря в колене(поворот), h_з-местная потеря в задвижке, h_р.р -местная потеря при резком расширении. Согласно Вейсбаху, h_к=ζ_к(v²/2g); h_з=ζ_з(v²/2g); h_р.р=ζ_р.р(v²/2g). Следовательно, Ʃh_j=( ζ_к+ ζ_з+ ζ_р.р) (v²/2g). В общем случае Ʃh_j=( v²/2g)Ʃ ζ_j. 2) потери напора по длине h_L. Эти потери выражаются формулой: h_L=λ(L/D)(v²/2g). Введём обозначение: (λL)/D= ζ_L. При этом h_L представится в виде h_L= ζ_L(v²/2g), где ζ_L можно назвать коэффициентом сопротивления по длине.3) полная потеря напора h_f получаем: h_f= ζ_L(v²/2g)+ ( v²/2g)Ʃ ζ_j, или h_f= (ζ_L+ Ʃ ζ_j )( v²/2g). Введём обозначение ζ_f= ζ_L+ Ʃ ζ_j. Получаем, что : h_f= ζ_f(v²/2g). Это и есть окончательная формула для расчёта полных потерь напора. Новый коэф. ζ_f, учитывающий все потери напора на данной длине потока, называется полным коэф. сопротивления. При помощи коэффициентов ζ соответствующие потери напора выражаются через скоростной напор.