Методы оценки точности.

Из большого разнообразия методов оценки точности рассмотрим чаще всего применяющиеся в производстве ЭА: наблюдение в цехах, статистический, расчетно-аналитический.

Метод наблюдения в цехах основан на сборе данных о точности изделий, получаемых при обработке и сборке, с использованием определенного оборудования и приспособлений, с учетом обрабатываемых материалов, инструментов и т. п. Эти данные систематизируют и сводят в таблицы экономической точности для различных методов обработки. Такие таблицы можно использовать для предварительной оценки точности разрабатываемого ТП.

Статистический метод оценки точности основан на положениях теории вероятности и математической статистики. Так как процесс производства ЭА характеризуется большим количеством факторов, влияющих на качество и требующих системного подхода к его анализу и синтезу, для исследования точности ТП используют различные статистические методы: кривых распределения, точечных и точностных диаграмм и др. Наиболее универсальным является метод кривых распределения,позволяющий оценить разброс погрешностей для данного ТП и определить процент возможного брака.

Рис.1.1. Гистограмма и полигон распределения параметров.

Для построения кривой распределения погрешностей следует замерить партию деталей (конкретный параметр, допустим, размер L) в количестве N = 100 шт. Замеренный параметр разбивается на равные интервалы и подсчитывается число и параметров в каждом интервале. Определяется частота m повторении отклонении параметров в партии m=n/N . Затем строится гистограмма и полигон распределения параметров (рис. 1.1). Устанавливается характер кривой распределения, исходя из критериев подобия Колмогорова. Вид кривой распределения зависит от характера погрешностей. Случайная погрешность подчиняется закону нормального распределения (закон Гаусса). Так, при работе на настроенных станках распределение случайных погрешностей имеет нормальный вид.

Кривые распределения случайных погрешностей характеризуются средним размером и средним квадратичным отклонением.Средний размер L_cp определяют по формуле

где L1,L2,Ln - размеры отдельных деталей; N - общее количество деталей в партии.

Среднее квадратичное отклонение    определяется выражением

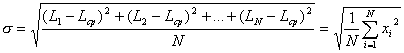
где xi=Li-Lср.

При вычислении значения L_cp и а в случаях большого числа размеров и партии удобнее группировать детали по интервалам размеров и проводить расчет по выражениям

где k - число интервалов;Li -размеры, соответствующие каждому интервалу; пi - количество деталей в каждом интервале;n1+n2+...+nk=N.

Для определения вероятностных характеристик важную роль играет количество деталей, которые нужно измерить, чтобы получить значения характеристик с достаточной степенью точности и достоверности. Для практических целей обычно бывает достаточно измерения 50...100 деталей. В тех случаях, когда столько деталей получить невозможно, вероятностные характеристики определяются по меньшему N, точность и достоверность результатов необходимо оценивать на основании методов математической статистики.

Ошибку Ɛ при определении среднеквадратического значения вычисляют по формуле

а при определении среднеарифметического значения

где Ɛ ошибка в долях σ _.

Из этих же выражений можно определить N, удовлетворяющее заданной точности.

Уравнение распределения Гаусса в координатах с началом в центре группирования имеет вид

где σ  - среднеквадратическое отклонение аргумента; е - основание натуральных логарифмов.

В зависимости от значения σ форма кривой нормального распределения меняется. Чем меньше σ тем уже кривая и поле рассеивания меньше; чем больше σ, тем кривая более пологая и поле рассеивания растет.

Кривая нормального распределения, асимптотически приближаясь к оси абсцисс, стремится к бесконечности в обе стороны, но, так как вне пределов промежутка Б3σ она почти сливается с осью абсцисс, то с достаточной для практики точностью теоретическую кривую заменяют кривой с полем рассеивания.

V=Б3 σ=6 σ=L_max-L_min

Площадь, ограниченная кривой нормального распределения и осью абсцисс, равна

Пользуясь кривой распределения погрешностей, можно найти вероятное количество годных деталей, на размер которых установлен определенный допуск σ _.

Вся площадь, ограниченная кривой распределения погрешностей, определяет полное количество деталей, обработанных при постоянной настройке оборудования.

Площадь кривой, соответствующая заданному интервалу отклонений х, определяется интегралом

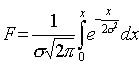
Этот интеграл обычно представляют в виде функции Ф(z), причем

Z=x/ σ

Дифференцируя это выражение, получим dx=σdz.

Подставляя значения z и dx, получаем

Величина Ф(z), называемая интегралом вероятностей Лапласа, для различных z приводится в справочной литературе.

Так как вся площадь, ограниченная кривой, равна единице, то значение Ф(z) определяет вероятность получения размера в пределахБх. При симметричном расположении поля допуска относительно поля рассеивания процент брака Р можно определить по формуле

Рис. 1.2. Обеспечение работы без брака.а - увеличением поля допуска; б - улучшением качества техпроцесса

Чтобы не было брака, следует либо увеличить допуск σ чтобы   (рис. 1.2, а), либо изменить ТП и уменьшить разброс погрешностей 6    (рис. 1.2, б).

Если имеет место систематическая постоянная погрешность, скажем, настройки оборудования _Δн, то форма кривой распределения не меняется, а происходит ее смещение на величину данной погрешности (рис.1.3, а). Если смешать две партии деталей, изготовленных при различных настройках оборудования, кривая распредел ения будет иметь вид, представленный на рис. 1.3, б.

Распределение систематических закономерно изменяющихся погрешностей происходит по различным законам в зависимости от изменения погрешностей. Если наряду со случайными имеются систематические закономерно изменяющиеся погрешности, то кривая распределения имеет вид, представленный на рис. 1.3, в.

Рис. 1.3. Виды кривых распределения.а - смещение кривой после поднастройки оборудования; б - случай смешения двух партий деталей; в -вариант случайно изакономерно изменяющейся погрешности.

Метод кривых распределения дает объективную картину распределения погрешностей для конкретного ТП. Зная величины средних и средне­квадратичных значений отклонений для различных ТП, можно заранее говорить о качестве получаемых изделий и проценте ожидаемого брака. Данный метод не учитывает последовательность обработки деталей, и отделить случайные погрешности от систематических не удается. Если это требуется и необходима большая наглядность в динамике погрешностей, используются точечные диаграммы. Замеряют параметры изделий в порядке их изготовления и наносят на диаграмму.

На практике замеряется группа параметров от 5—10 штук в последовательности их изготовления, определяется их среднее значение и наносится на диаграмму (рис. 1.4).

Рис. 1.4. Пример построения диаграммы статистического контроля параметра

Получаем диаграмму статистического контроля, которая дает возможность работать без брака, так как время появления параметров, выходящих за контрольную зону А, видно по диаграмме. Контрольная зона А меньше поля допуска из-за малой величины выборки для определения среднего значения параметра на величину

поля рассеивания среднегрупповых значений параметров, где т — величина выборки (т - 5 - 10).

Точностные диаграммы (рис. 1.5) -это дальнейшее развитие точечных диаграмм, которые дают более точную картину изменения погрешностей во времени и выявить

Рис. 1.5. Пример построения точностной диаграммы.

закономерность изменения переменных система­тических погрешностей.

Порядок построения точностных диаграмм такой же, как и для точечных диаграмм, но выборки последовательно замеряемых параметров увеличиваются до 25 в группе. Для данной выборки строится кривая распределения, и определяются основные статистические параметры: среднее и среднеквадратичное отклонение, поле рассеивания и т. д.

Точностная диаграмма дает возможность установить закон распределения параметров во всей партии изделия для конкретного технологического процесса. Например, L_ср=f(n) - закон изменения среднеарифметических значений параметра.

Статистические методы позволяют вскрыть источники погрешностей, возникающих в процессе производства, определить закон изменения систематических, величины этих погрешностей и время поднастройки работы оборудования.