Силы трения

Силы, возникающие между поверхностями соприкасающихся тел, и препятствующие их относительному перемещению, называются силами трения. Параллельным переносом силу трения рисуют из точки центра тяжести тела. Она направлена против скорости относительного перемещения тел.  Внешним или сухим трением называется трение, возникающее между твердыми телами. В свою очередь оно подразделяется на трение покоя и кинематическое трение (скольжения и качения). Сила трения покоя равна максимальной силе, которую следует приложить к твердому телу, чтобы только началось его перемещение. F_тр = kN Здесь N – сила нормального давления. к Зависимость коэффициента  трения от скорости переме- щ ения тел показана на рисунке. При малых  с коростях перемещения V коэффициент трения сколь- жения и качения меньше коэффициента трения покоя. Трение покоя связано с упругим деформированием взаимодействующих тел. Трение скольжения и качения связаны с неупругим деформированием поверхностей тел и даже их частичным разрушением. Поэтому кинематическое  трение сопровождается акустической эмиссией – шумом. Тр ение качения связано с неупругим деформированием тел. Тогда  во зникает горизонтальная составляющая  си лы реакции на деформирование N₂ по верхности под передней частью колеса – N₁ это и есть сила трения качения. N₂  N₁ . Способы уменьшения коэффициента трения:

1. Замена трения скольжения трением качения.

2. Замена сухого трения – вязким.

3. Повышение качества обработки поверхностей трущихся деталей.

4. Замена трения покоя – трением скольжения и трением качения путем применения звуковых и ультразвуковых вибраций.

5. Использование полимернаполненных композиций на основе фторопласта.

6.   Гравитационное взаимодействие − самое слабое из четырёх фундаментальных взаимодействий. Согласно закону всемирного тяготения Ньютона сила гравитационного взаимодействия F_g двух точечных масс m₁ и m₂ равна

7. 

8.     G = 6.67·10^-11 м³· кг^–1·см^–2 − гравитационная постоянная, r − расстояние между взаимодействующими массами m₁ и m₂. Отношение силы гравитационного взаимодействия между двумя протонами к силе кулоновского электростатического взаимодействия между ними равно 10^-36.      Величина G^1/2·m называется гравитационным зарядом. Гравитационный заряд пропорционален массе тела. Поэтому для нерелятивистского случая согласно закону Ньютона ускорение, вызываемое силой гравитационного взаимодействия F_g, не зависит от массы ускоряемого тела. Это утверждение составляет принцип эквивалентности.     Фундаментальное свойство гравитационного поля состоит в том, что оно определяет геометрию пространства-времени, в котором движется материя. По современным представлениям взаимодействие между частицами происхо­дит путём обмена между ними частицами – переносчиками взаимодействия. Считается, что переносчиком гравитационного взаимодействия является гравитон − частица со спином J = 2. Экспериментально гравитон не обнаружен. Квантовая теория гравитации пока не создана.

Все наши ежедневные действия сводятся к тому, что мы с помощью мышц либо приводим в движение окружа­ющие тела и поддерживаем это движение, либо же оста­навливаем движущиеся тела.

Этими телами являются орудия труда (молоток, ручка, пила), в играх — мячи, шайбы, шахматные фигуры. На производстве и в сельском хозяйстве люди также приво­дят в движение орудия труда. Правда, в настоящее время роль рабочего все больше и больше сводится к управлению механизмами. Но в любой машине можно обнаружить по­добие простых орудий ручного труда. В швейной машинке имеется игла, резец токарного станка подобен рубанку, ковш экскаватора заменяет лопату.

Двигатели. Применение машин во много раз увеличи­вает производительность труда благодаря использованию в них двигателей.

Назначение любого двигателя в том, чтобы приводить тела в движение и поддерживать это движение, несмотря на торможение как обычным трением, так и «рабочим» со­противлением (резец должен не просто скользить по ме­таллу, а, врезаясь в него, снимать стружку; плуг должен взрыхлять землю и т. д.). При этом на движущееся тело должна действовать со стороны двигателя сила, точка при­ложения которой перемещается вместе с телом.

Бытовое представление о работе. Когда человек (или какой-либо двигатель) действует с определенной силой на движущееся тело, то мы говорим, что он совершает работу. Это бытовое представление о работе легло в основу форми­рования одного из важнейших понятий механики — поня­тия работы силы.

Работа совершается в природе всегда, когда на какое-либо тело в направлении его движения или против него действует сила (или несколько сил) со стороны другого тела (других тел). Так, сила тяготения совершает работу при падении капель дождя или камня с обрыва. Одновре­менно совершают работу и силы трения, действующие на падающие капли или на камень со стороны воздуха. Со­вершает работу и сила упругости, когда распрямляется со­гнутое ветром дерево.

Определение работы. Второй закон Ньютона в форме   позволяет определить, как меняется скорость тела   по модулю и направлению, если на него в течение времени ∆tдействует сила  .

Во многих случаях важно уметь вычислять изменение скорости по модулю, если при перемещении тела на   на него действует сила . Воздействия на тела сил, приводя­щих к изменению модуля их скорости, характеризуются величиной, зависящей как от сил, так и от перемещений тел. Эту величину в механике и называют работой силы.

В общем случае при движении твердого тела перемеще­ния его разных точек различны, но при определении работы силы мы под   понимаем перемещение ее точки при­ложения. При поступательном движении твердого тела перемещение всех его точек совпадает с перемещением точки приложения силы.

Сила, перпендикулярная скорости (а следовательно, и перемещению  ), изменяет скорость только по направ­лению, но не по модулю. (При равномерном движении по окружности ускорение тела, а следовательно, и действующая на него силаперпендикулярны скорости.)

Изменение скорости по модулю возможно лишь в том случае, когда проекция силы на направление перемещения тела F_r отлична от нуля. Именно эта проекция определяет действие силы, изме­няющей скорость тела по модулю. Она совершает работу. Поэтому работу можно рассматривать как произведение проекции F_r на модуль перемещения   (рис. 1):

A = F_r . (1)

Если угол между силой и перемещением обозначить через α, тоF_r = F·cos α. Следовательно, работа равна:

А = F  cos α. (2)

Работа силы равна произведению модулей силы иперемещения точки приложения силы и косинуса угла меж­ду ними.

Формула (1) справедлива в том случае, когда сила по­стоянна и перемещение тела происходит вдоль прямой. В случае криволинейной траектории и переменной силы мы разделяем траекторию на малые отрезки, которые можно считать прямолинейными, а силу на них постоян­ной.

Работа, в отличие от силы и перемещения, является не векторной, а скалярной величиной. Она может быть поло­жительной, отрицательной или равной нулю.

З нак работы определяется знаком косинуса угла между силой и перемещением. Если α < 90°, то А > 0, так как ко­синус острых углов положителен. При α > 90° работа отри­цательна, так как косинус тупых углов отрицателен. При α = 90° (сила перпендикулярна перемещению) работа не совершается. Так, сила тяжести не совершает работу при перемещении тела по горизонтальной плоскости. При движении спутника по круговой орбите сила тяготения также не совершает работу.

Если на тело действует несколько сил, то проекция ре­зультирующей силы на перемещение равна сумме проек­ций отдельных сил:

F_r = F_1r + F_2r + … (3)

Поэтому для работы результирующей силы получаем

А = F_1r  + F_2r   + …=А₁+А₂+…

Итак, если на тело действует несколько сил, то полная работа (сумма работ всех сил) равна работе результирую­щей силы.

Совершенную силой работу можно представить графи­чески. Поясним это, изобразив на рисунке зависимость проекции силы от координаты тела при его движении по прямой.

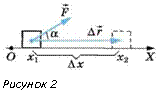
Пусть тело движется вдоль оси ОХ (рис. 2), тогда F cos α = F_x,\ \= ∆х.

Для работы силы получаем:

А = F | | cos α = F_x∆х.

Очевидно, что площадь прямо­угольника, заштрихованного на ри­сунке 3, численно равна работе при перемещении тела из точки с координатой x₁ в точку с коорди­натой х₂.

Единица работы. Единицу рабо­ты можно установить с помощью основной формулы (2). Если при перемещении тела на единицу дли­ны на него действует сила, модуль которой равен единице, и направ­ление силы совпадает с направлением перемещения (α = 0), то и paбота будет равна единице. В Международной системе еди­ниц (СИ) работа измеряется в джоулях (обозначается Дж):

1Дж=1Н·1м = 1Н·м.

Итак, джоуль — это работа, совершаемая силой 1Н на перемещении 1 м, если направления силы и перемещения совпадают.

Часто используют кратную единицу работы — килоджоуль:

1 кДж = 1000 Дж.

Приведено определение работы силы   при перемещении тела на  , составляющем угол α с направлением силы: А = F | | cos α.

Очень часто важно знать не только работу, но и время, в течение которого она произведена. Поэтому надо ввести еще одну величину — мощность.

Работа может быть совершена как за большой проме­жуток времени, так и за очень малый. На практике, одна­ко, далеко не безразлично, быстро или медленно может быть произведена работа. Временем, в течение которого совершается работа, определяют производительность лю­бого двигателя. Очень большую работу может совершить и крошечный электромоторчик, но для этого понадобится много времени. Потому наряду с работой вводят величину, характеризующую быстроту, с которой она производит­ся, — мощность.

Мощностью называют отношение работы А к интерва­лу времени ∆t, за который эта работа совершена:

 (4)

Иными словами, мощность численно равна работе, со­вершенной в единицу времени.

Подставляя в формулу (4) вместо работы А ее выра­жение (2), получим

 (5)

Таким образом, мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов.

Понятие мощности вводится для оценки работы за еди­ницу времени, совершаемой каким-либо механизмом (насо­сом, подъемным краном, мотором машины и т. д.). Поэто­му в формулах (4) и (5) под   всегда подразумевается сила тяги.

В СИ мощность выражается в ваттах (Вт). Мощность равна 1 Вт, если работа 1 Дж совершается за 1 с.

Наряду с ваттом используются более крупные (крат­ные) единицы мощности:

1 гВт (гектоватт) = 100 Вт,

1 кВт (киловатт) = 1000 Вт,

1 МВт (мегаватт) = 1 000 000 Вт.