§8. Третий закон Ньютона

Третий закон Ньютона утверждает, что в инерциальных системах отсчёта  независимо от того движутся взаимодействующие тела или находятся в относительном покое; силы, с которыми два тела действуют друг на друга, равны по модулю, противоположны по направлению и приложены соответственно к взаимодействующим телам.

Если тело А действует на тело В с силой  (рис.16), то одновременно на тело В со стороны тале А будет действовать сила  , причём   (3)

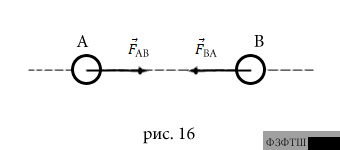
Силы взаимодействия приложены к разным телам и, следовательно не могут уравновешиваться. Их нельзя складывать или вычитать.

3-й закон Ньютона распространяется и на систему из произвольного числа взаимодействующих тел. Просто в этом случае следует рассматривать силы попарного взаимодействия между телами системы.

ПРИМЕР 17. Мяч ударяется о стенку. На какое из тел (мяч или стенку) действует при ударе бóльшая сила? Выберите правильное утверждение.

1. На мяч бóльшая.

2. На стенку бóльшая.

3. На оба тела действуют одинаковые по модулю силы.

ОТВЕТ. Правильные вариант 3). По 3-му закону Ньютона первые два варианта отпадают.

ПРИМЕР 18. В результате взаимодействия двух тел массами   и   первое тело приобрело ускорение  . Чему равно ускорение  , приобретённое вторым телом?

РЕШЕНИЕ. По 3-му закону Ньютона силы, с которыми взаимодействуют тела удовлетворяют равенству (3). С учётом 2-го закона Ньютона это равенство  можно переписать в виде:  . Отсюда для модулей ускорений тел следует, что  . Из этого равенства легко находим  :  ; Направление ускорения   противоположно направлению ускорения 

Фундаментальные и нефундаментальные взаимодействия

Естествоиспытатели и философы прошлого и настоящего времени пытались объяснить многообразие явлений природы с единых позиций. Так и в физике учёные стремились свести реальные силы к конечному числу фундаментальных взаимодействий. В настоящее время фундаментальными называют четыре типа взаимодействий, к которым сводятся все остальные.

1. Сильное или ядерное взаимодействие U = De^-r/r. Здесь =1/r_o 

r_o 10^-14 м – характерное расстояние, на котором проявляется действие ядерных сил. Взаимодействие короткодействующее (на малых расстояниях), носит характер притяжения.

2. Электромагнитное взаимодействие U_кул = q₁q₂/r – дальнодействующее, носит характер притяжения в случае разноимённых зарядов. Отношение интенсивностей электромагнитного и ядерного взаимодействий I_эм/I_яд = 10^-2. 

3. Слабое взаимодействие – короткодействующее I_сл/I_яд = 10^-14.

4. Гравитационное взаимодействие – дальнодействующее 

I_грав/I_яд = 10^-39 . U_грав =Gm₁m₂/r – взаимодействие носит характер притяжения.

Реальные силы. Силы упругости и силы трения

Силы упругости. Силы упругости возникают как реакция на деформирование твердого тела. Определим некоторые понятия. Деформация (  )– относительное смещение точек тела. Упругое напряжение (  ) – давление, возникающее в твердом теле при его деформировании  = F/S. Здесь S – площадка, на которую действует сила упругости F. Связь между напряжением и деформацией следующая:  I – область  с оответствует упругим д еформациям. Здесь  справедлив закон Гука: , где Е - модуль I II III упругости. I I – область неупругих

• деформаций.

III – область разрушения материала. Для тел стержнеобразной формы (стержни, балки, трубы)  = L/L – относительное удлинение, Е – модуль Юнга. Сдвиговые напряжения _ связаны со сдвиговыми деформациями _= D/D (D – диаметр стержня) через модуль сдвига G: _ = G_. Гидродинамическое давление Р связано с относительным изменением объема через модуль всестороннего сжатия К:  Р = КV/V. Для изотропных тел независимыми модулями упругости будут только два. Остальные могут быть пересчитаны по известным формулам, например: Е = 2G(1 + ). Здесь  - коэффициент Пуассона. Природа сил упругости связана с фундаментальными электромагнитными взаимодействиями.