Неравенство чебышева
Теорема 3. Пусть x– с вероятностью 1 неотрицательная сл. величина, имеющая конечное математическое ожидание. Тогда
(4.3)
Доказательство.
Введем в
рассмотрение событие
.
Для него индикаторная функция имеет
вид:
.
Согласно свойству М8 математического
ожидания
.
Рассмотрим теперь очевидное неравенство
любое положительное число. Тогда
или
или
.
Доказанное неравенство известно под названием неравенства Чебышева.
Следствие. Для произвольной сл. величины x , имеющей дисперсию Dx,
(4.4)
Именно это
неравенство известно широкому кругу
читателей под названием неравенства
Чебышева. Оно получается из теоремы 3,
если в качестве неотрицательной сл.
величины взять
Неравенство
эквивалентно неравенству
.
Поэтому
.
Однако, неравенство
(4.4) может быть доказано и без помощи
теоремы 3. Введем в рассмотрение сл.
величину
. Тогда
Но
Следовательно,
и
Неравенство (4.4)
следует применять, когда
,
иначе оно дает тривиальную оценку.
Пример 1. Пусть
сл. величина x
имеет
плотность распределения
.
Тогда Mx=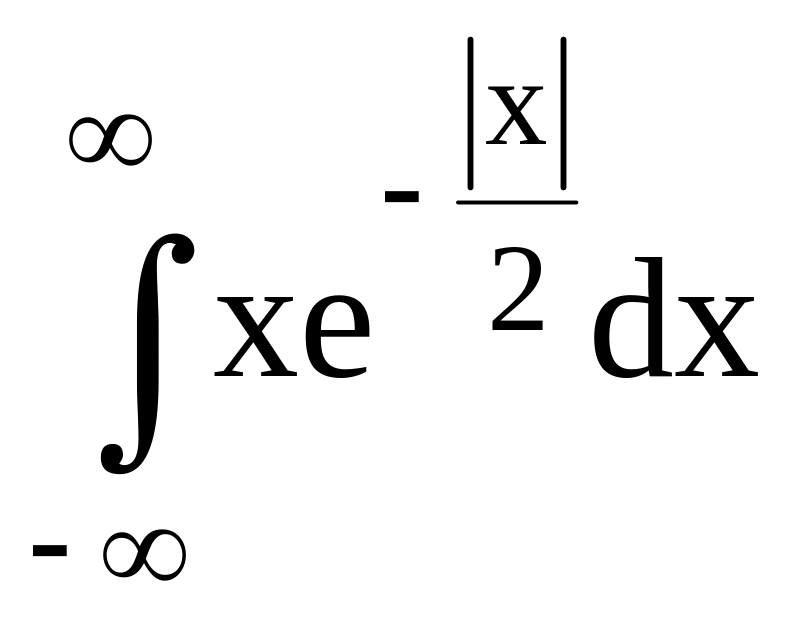
=0
(интеграл от нечетной функции по
симметричному множеству),
(нтегрировали по частям).
Оценим
при
e=1,2,
5, 10. Получим
.
Прямое вычисление величин
при заданных значениях ε дает выражения
,
.
Видим, что неравенство Чебышева дает довольно грубые оценки вероятностей. Однако неравенство Чебышева является родоначальником многих других неравенств, широко применяемых в теории вероятностей.
4.4. Типы сходимости
Пусть дана некоторая
последовательность сл. величин
и сл. величина x.
Определение.
Говорят, что
последовательность сл. величин
сходится
к сл. величине x
почти
наверное (с
вероятностью 1),
если
Обозначение:
или
Иначе говоря,
равенство
означает, что множество тех w,
для которых последовательность
имеет вероятностную меру 0.
Определение.
Говорят, что
последовательность сл. величин
сходится
к сл. величине x
по
вероятности,
если
.
Обозначение:
или
В отличие от
предыдущего случая сходимость по
вероятности означает, что существуют
множества значений ω ненулевой
вероятности, для которых
не имеет пределом
при n→∞.
Эти два вида
сходимости связаны между собой: из
сходимости почти наверное следует
сходимость по вероятности. Обратное
утверждение не имеет места, но если
последовательность
,
то любая её подпоследовательность
содержит
другую подпоследовательность, сходящуюся
по вероятности 1 [3].
Определение.
Говорят, что
последовательность сл. величин
сходится
к сл. величине x
в среднем
порядка p, если
.
В анализе этот вид
сходимости называют сходимостью в
смысле
.
Поэтому обозначают этот вид сходимости
так:
.
При p
= 2
сходимость
называют сходимостью в среднем
квадратическом, обозначают это так:
(от limit
in
the
mean)
или
.
Определение.
Пусть сл.
величины
имеют
функции распределения
,
а сл. величина x
– F(x).
Говорят, что последовательность сл.
величин
сходится
по распределению
к сл. величине
x,
если
во всех точках непрерывности функции
F.
Обозначение:
Говорят ещё в этом
случае, что последовательность функций
распределения
слабо сходится к функции распределения
:
.
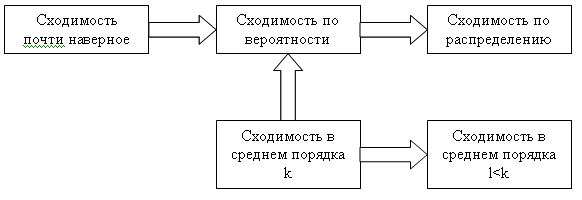
Соотношения между различными типами сходимости представлены ниже в виде схемы:
