11. Характеристики случайной величины: дисперсия и среднее квадратическое отклонение. Свойства дисперсии.

 Дисперсией   случайной величины   называется математическое ожидание квадрата отклонения случайной величины от ее математичекого ожидания *:

(43)

   Пусть   - дискретная случайная величина, принимающая значения x₁, x₂, ..., x_n соответственно с вероятностями p₁, p₂, ..., p_n. Очевидно, случайная величина   принимает значения

с теми же вероятностями p₁, p₂, ..., p_n. Следовательно, согласно определению математического ожидания дискретной случайной величины, имеем

(44)

   Если же   - случайная величина с плотностью распределения  , то по определению

(45)

   Принимая во внимание определение дисперсии и свойства математического ожидания, имеем

   Так как   и   - постоянные, то используя свойства математического ожидания, получим

   Следовательно,

   Откуда окончательно находим

(46)

   Рассмотрим теперь свойства дисперсии.     1°. Дисперсия постоянной равна нулю.

Пусть  . По формуле (46) имеем

   так как математическое ожидание постоянной есть эта постоянная:

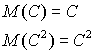
   2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

(47)

  Доказательство. На основании соотношения (46), можно записать

   Так как    и

   то

   3°. Если   и   - независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий:

(48)

   Но

   Так как   и   - независимые случайные величины, то

   Следовательно

   Далее,

   поэтому

   Таким образом

   Следовательно

   Замечание. Свойство 3° распространяется на любое конечное число попарно независимых случайных величин:

   Средним квадратическим отклонением   случайной величины   называется корень квадратный из ее дисперсии:

(49)

 Среднее квадратическое отклонение   имеет ту же размерность, что и случайная величина  . 

12. Биноминальный закон распределения случайной величины, его свойства, характеристики случайной величины, полигон распределения.

3.1 Биномиальное распределение

Биномиальным называют закон распределения дискретной случайной величины X - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события постоянна. Вероятности p_iвычисляют по формуле Бернулли

Для биномиального распределения: математическое ожидание M(X) = np, дисперсия D(X) = npq, мода np-q ≤ Mo ≤ np+p, коэффициент асимметрии As = (q - p)/√npq, коэффициент эксцесса Ex = (1 - 6pq)/npq В пределе при n→∞ биномиальное распределение по своим значениям приближается к нормальному с параметрами a=np и σ=√npq В пределе при n→∞ и при p→0 биномиальное распределение превращается в распределение Пуассона с параметром λ=np.