7. Случайная величина. Виды случайных величин.

Понятие случайной величины является основным в теории вероятностей и ее приложениях. Случайными величинами, например, являются число выпавших очков при однократном бросании игральной кости, число распавшихся атомов радия за данный промежуток времени, число вызовов на телефонной станции за некоторый промежуток времени, отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе и т. д.     Таким образом, случайной величиной называется переменная величина, которая в результате опыта может принимать то или иное числовое значение.     В дальнейшем мы рассмотрим два типа случайных величин — дискретные и непрерывные.     1. Дискретные случайные величины.     Рассмотрим случайную величину *  , возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2, ..., xn, ... . Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1,2, ...) равно вероятности того, что величина  примет значение xi

(16)

   Такая случайная величина  называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2, ..., xn, ... . Так как в каждом из испытаний случайная величина  принимает всегда какое-либо значение из области ее изменения, то

Абсолютно непрерывные случайные величины

Если функция распределения случайной величины   имеет вид:

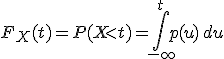, где   - интегрируемая неотрицательная функция,

тогда эта случайная величина называется абсолютно непрерывной. Функция   при этом называется плотностью распределения. Плотность распределения удовлетворяет свойствам:

 и  .

И наоборот, любая интегрируемая функция  , удовлетворяющая этим свойствам, может быть взята в качестве плотности распределения некоторой случайной величины.

Поскольку функция распределения является функцией верхнего предела от плотности, то последняя восстанавливается по ней дифференцированием:

8. Интегральная функция распределения случайной величины, её свойства.

9. Дифференциальная функция распределения случайной величины (плотность распределения вероятности), её свойства. Выражение интегральной функции через дифференциальную функцию распределения случайной величины.

Дифференциальная функция распределения

Дифференциальная функция распределения  непрерывных случайных величин f(x) и ее свойства.

Способ, когда закон распределения непрерывной случайной величины задают с помощью интегральной функции, не является единственным. Гораздо чаще его задают с помощью дифференциальной функции распределения вероятностей, которую обозначают f(x). Эту функцию также называют плотностью распределения вероятностей.

Дифференциальной функцией распределения называется 1-я производная от интегральной функции распределения .

Для дискретной случайной величины функция распределения будет иметь разрывы, и поэтому она не применяется для дискретных величин.

Теорема: Вероятность того, что непрерывная случайная величина Х примет значение на интервале (а,b) равна определенному интегралу от дифференциальной функции, взятому в  этих пределах

Доказательство:   Будем исходить  из известного:   P(a <Х < b) = F(b)–F(a)  Отсюда ,  если      где      z – переменная интегрирования.

 

Свойства дифференциальной функции распределения

 

1.  , т.к. это производная от неубывающей функции. 2.  , следует из доказательства теоремы, f (x) dx       элемент вероятности. 3.            .

10. Характеристики случайной величины: математическое ожидание. Свойства математического ожидания.    Математическим ожиданием   дискретной случайной величины   называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е. *

(39)

   Возвращаясь к разобранному выше примеру, мы видим, что средний диаметр подшипника равен математическому ожиданию случайной величины   - диаметру подшипника.     Математическим ожиданием   непрерывной случайной величины   с плотностью распределения   называется число, определяемое равенством

(40)

   При этом предпологается, что несобственный интеграл, стоящий в правой части равенства (40) существует.     Рассмотрим свойства математического ожидания. При этом ограничимся доказательством только первых двух свойств, которое проведем для дискретных случайных величин.     1°. Математическое ожидание постоянной С равно этой постоянной.     Доказательство. Постоянную C можно рассматривать как случайную величину  , которая может принимать только одно значение C c вероятностью равной единице. Поэтому       2°. Постоянный множитель можно выносить за знак математического ожидания, т.е.

   Доказательство. Используя соотношение (39), имеем

   3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:

(41)

   4°. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин **: