1. Основные понятия и определения теории вероятностей. Виды случайных событий. Классическое и статистическое определение вероятности события. Свойства вероятностей события. Непосредственный подсчет вероятностей. Основные формулы комбинаторики.

Теория вероятности- математическая наука, занимающаяся изучением закономерностей в случайных явлениях массового характера.

Основное понятие в ТВ является – событие.

Под событием понимается явление, которое происходит в результате осуществления какого-либо комплекса условий, воспроизводящие неограниченное число раз.

Осуществление этого комплекса условий называется испытанием или опытом.

Случайное событие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.

С теоритической точки зрения второстепенные факторы случайны ни чем не отличаются от основных, точность за счет учета как можно большего кол-ва фактов.

Существуют принципиальная разница в методах учета этих факторов.

1 подход: классический выделяет основные определяющие факторы, а множество второстепенных инспирируется, формир основную закономерность, позволяющую однозначно предсказать рез-т по заданным условиям.

2 подход: с изучением элементов неопределен.(Вероятностный подход) основывается на основных фактов, учитывается влияние неопределенности.

Виды событий.

1.Случайным называется событие, которое может произойти или не произойти в результате проведения эксперимента. Случайные события обозначаются первыми буквами латинского алфавита: А, В, С,... .

2.СОВМЕСТНОЕ СОБЫТИЕ В теории вероятности – любое событие, которое представляет собой одновременное возникновение любых двух (или более) других событий

3.несовместимыми событий называются, если никакие два из них не могут появиться одновременно в результате однократного испытания случайного эксперимента.

4.Достоверным называется событие, которое обязательно произойдет в результате проведения эксперимента. Достоверное событие обозначается буквой  .

5.Невозможным называется событие, которое заведомо не произойдет в результате проведения эксперимента. Оно обозначается символом пустого множества: Æ.

6.противоположным событию А, называется событие, обозначаемое   которое происходит тогда и только тогда, когда не происходит событие А.

7.Взаимодополняющие события- это 2 события А и , называются если 1 из них в рез-те опыта влечет не появление другого

8.РАВНОВОЗМОЖНЫЕ СОБЫТИЯ-   События называют равновозможными, если имеются основания считать, что ни одно из этих событий не является более возможным, чем другие.

9.Не равновозможные события-это события, вероятность их появления не равна

Действия над событиями

Суммой (или объединением) событий называется событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из данных событий.

Обозначения суммы событий:

алгебраические: , теоретико-множественные: 

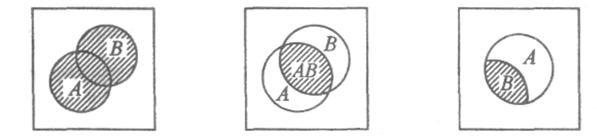
На диаграмме сумма событий А и В изображается областью, которая накрывается областями, изображающими события А и В (рис. 1).

Произведением (пересечением) событий называется событие, происходящее тогда и только тогда, когда все данные события происходят вместе (одновременно).

Обозначения произведения событий:

алгебраические:  , теоретико-множественные:  .

На диаграмме произведение событий АВ изображается общей ча­стью областей, изображающих события А и В (рис. 2).

рис.1 рис. 2 рис. 3

Разностью двух событий А и В называется событие, состоящее в том что событие А произошло, исключая появления события В.

На диаграмме не заштрихованная область А является разностью событий А и В. (рис. 3).

Свойства операций сложения, умножения, дополнения:

1.  ;

2.  ;

3.  ;

4.  .

События называются несовместными (или зависимыми), если их произведение есть невозможное событие, т.е. не могут совместно произойти.

Если события попарно несовместны, то несовместны и в совокупности.

Полной группой событий называется множество событий, сумма которых есть достоверное событие:  . В частности,  .

Основные правила комбинаторики. Приведем наиболее употребительные из них.

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

P_n = n!, где n! = 1 * 2 * 3 ... n.

Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений

A^m_n = n (n - 1)(n - 2) ... (n - m + 1).

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

С ^m_n = n! / (m! (n - m)!)

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

A^m_n = P_mC ^m_n.

З а м е ч а н и е. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., то число перестановок с повторениями

P_n (n₁, n₂, ...) = n! / (n₁! n₂! ... ), где n₁ + n₂ + ... = n.

При решении задач комбинаторики используют следующие правила:

П р а в и л о   с у м м ы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

П р а в и л о   п р о и з в е д е н и я. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.

2. Сложные события. Сумма и произведение событий. Теорема сложения вероятностей для несовместных событий и следствия из нее. Теорема сложения вероятностей для совместных событий.

Сумма событий. Суммой событий А1, А2, ..., Аn называется событие А = А1+А2+ ...+ Аn, состоящее в наступлении хотя бы одного из событий А1, А2, ..., Аn. Например, два стрелка стреляют в одну и ту же мишень по одному разу. Обозначим события: А1: "1-й стрелок попал в мишень", А2: "2-й стрелок попал в мишень". Тогда их суммой будет событие А: "Мишень поражена", то есть, либо попал только 1-й стрелок, либо только 2-й, либо попали оба.

Пусть события A и В — несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие A, либо событие В? Ответ на этот вопрос дает теорема сложения.

Произведение событий. Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А — деталь годная, В — деталь окрашенная, то АВ — деталь годна и окрашена.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С — появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то АВС — выпадение «герба» во всех трех испытаниях.

Теорема сложения вероятностей для несовместных событий и следствия из нее

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В).

Доказательство

Введем обозначения: n — общее число возможных элементарных исходов испытания; m₁ — число исходов, благоприятствующих событию A; m₂— число исходов, благоприятствующих событию В.

Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m₁ + m₂. Следовательно,

Р (A + В) = (m₁ + m₂) / n = m₁ / n + m₂ / n.

Приняв во внимание, что m₁ / n = Р (А) и m₂ / n = Р (В), окончательно получим

Р (А + В) = Р (А) + Р (В).

С л е д с т в и е. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (A₁ + A₂ + ... + A_n) = Р (A₁) + Р (A₂) + ... + Р (A_n).

Теорема сложения для совместных событий

 Суммой 2-х совместных событий называют событие, состоящее в появлении либо события A, либо события B, либо обоих сразу.

 Теорема. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без учета их совместного появления. p(A+B)=p(A)+p(B)−p(AB) 

Доказательство:

A+B=AB+AB+AB (сумма несовместных пар)

Тогда p(A+B)=p(AB)+p(AB)+p(AB)

Событие A=AB+AB,

Событие B=AB+AB

p(A+B)=p(A)−p(AB)+p(B)−p(AB)+p(AB)=p(A)+p(B)−p(AB) 

 

Замечание: в этой теореме может существовать 2 различные ситуации.

p(A+B)=p(A)+p(B)−p(A)p(B),  где A и B - независимые;

p(A+B)=p(A)+p(B)−p(A)p(B∖A),  где A и B - зависимые;

3. Зависимые и независимые события. Условная вероятность события. Теорема умножения вероятностей для конечного числа зависимых событий. Теорема умножения вероятностей для конечного числа независимых вероятностей

 Зависимыми события называют если вероятность появления одного из них зависит от наступления или ненаступления другого события.

Независимыми события называют если вероятность появления одного из них не зависит от наступления или ненаступления другого события

Условная вероятность

Условной вероятностью Р_A (В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Исходя из классического определения вероятности, формулуР_A (В) = Р (АВ) / Р (А) (Р (А) > 0 можно доказать. Это обстоятельство и служит основанием для следующего общего (применимого не только для классической вероятности) определения.

Условная вероятность события В при условии, что событие А уже наступило, по определению, равна

Р_A (В) = Р (АВ) / Р (А)    (Р(A)>0).

Теорема умножения для зависимых событий

Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: 

P (AB) = P (A)*PA(B).

Теорема умножения для независимых событий

Теорема. Вероятность произведения двух независимых событий А и В равна произведению их вероятностей: 

P(AB) = P(A)*P(B).