Екзамен.Білет № 28

4.Розв’язати транспортну задачу:

ai = (10; 80; 15); bj = (75; 20; 50);

.

Задача розв.методом потенціалів. Початковий план знайдений методом Пн.-Зх. кута. Виділені ячейки вказують на значення, які переносяться з попереднього опорного плану, що відповідають табл., вказаній в умові відповідно. Задача не збалансована, тому вводиться фіктив.

5.Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

, .

Перетворюємо до вигляду Лагранжа:

x1 = 3 – 2x2

2x2 – 2x1 + 2 = x1 – 4x2 + 2

2x2 – 6 + 4x2 + 2 = 3 – 2x2 – 4x2 +2

12x2 = 9

x1 = 1,5 x2 = 0,75

Знаходимо вид екстремуму:

Немає знакозмінного ряд, тому екстремум функції досягається у мінімумі. Значення функції: Z = 6.25

6. Орендне підприємство має можливість укласти дві різні угоди: першу угоду з фірмою в цьому ж місті, другу – з фірмою іншого міста, але з більш вигідними поставками. Можливі два варіанти прибутку при виборі першої фірми: 9000 гривень, якщо фірма буде мати змогу вкласти нову угоду, 7000 гривень , якщо це буде одинична поставка. При виборі другої фірми: 13000 гривень та 7500 гривень з урахуванням поставок. Результати та відповідні їм ймовірності наведені в таблиці. Вибрати найменш ризиковане рішення та оцінити величину ризику.

Варіанти вибору фірми	Результат 1		Результат 2
	ймовірність	прибуток	ймовірність	Прибуток
1	0,7	9000	0,3	7000
2	0,4	13000	0,6	7500

Екзам. Білет №29

4. На виготовлення двох видів продукції (П₁ і П₂) витрачаються три види ресурсів Наявність ресурсів дорівнює відповідно: 361, 520, 248. Витрати ресурсів на одиницю продукції П₁ становлять відповідно:13, 7, 17; на одиницю продукції П₂ - 16, 4, 9. Ціна за одиницю продукції дорівнює відповідно: 11, 8. Побудувати модель лінійного програмування початкової й двоїстої задач. Знайти такий план виробництва, який би забезпечував найбільшу виручку. Дати економічне тлумачення розв’язків задач.

Пряма задача:

;

;

;

;

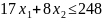Вводимо 3 штучні змінні і складаємо симплексну таблицю:

Значення цільової функції: Z = 31213\155 або 201,4

x1 = 719\155 або 4,63

x2 = 2913\155 або 18,8

Двоїста задача:

;

;

;

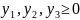
Компоненти вектора Y^* (оптимальний план двоїстої задачі) визначимо за формулою:

де та міститься в стовпчику «БП» останньої симплекс-таблиці;

Y = 201.4

4. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування, визначити характер екстремуму:

, .

Перетворюємо до вигляду Лагранжа:

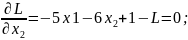
x1 = x2 + 5

4x1 + 5x2 +2 = -5x1 – 6x2 + 1

4x2 + 20 +5x2 + 2 = -5x2 – 25 – 6x2 +1

20x2 = -46

x2 = -2,3 x1 = 2,7

Знаходимо вид екстремуму:

Значення функції Z = -3,1

4. На ринку дві конкуруючі корпорації намагаються стати лідерами і контролювати всі дрібні компанії своєї галузі. Невелика фірма може опинитись в результаті такої політики в складі однієї з цих двох корпорацій, що може принести їй, як вдачу, так і збитки. З метою протистояння корпораціям, фірма може виступити ініціатором створення асоціації дрібних підприємств своєї галузі, що може привести до досить великого успіху, але є досить ймовірною також невдача від цієї діяльності. Який з трьох варіантів вибрати фірмі?

Варіанти злиття	Успіх		Невдача
	Ймовірність	Прибуток, млн.грн.	Ймовірність	Прибуток, млн.грн
1 корпорація	0,6	8	0,4	0,5 млн.
2 корпорація	0,7	12	0,3	0,5 млн.
Створення асоціації	0,3	25	0,7	1 млн.