11.Ключевая идея дп. Принцип оптимальности Беллмана.

Динамическое программирование — раздел математического программирования, представляет собой совокупность приемов, позволяющих находить оптимальные решения, основанные на вычислении последствий каждого решения и выработке оптимальной стратегии для последующих решений.

Ключевая идея –решить поставленную задачу с помощью деления задачи на подзадачи, решения подзадач, а затем объединение решений подзадач в общее решение.

Процессы принятия решений , которые строятся по такому принципу, называются многошаговыми. Общим для задачи динамического программирования явл-ся то, что переменные рассматриваются не вместе, а последовательно одна за другой.

Всё это вытекает из принципа оптимальности Беллмана, лежащего в основе теории динамического программирования.

Принцип оптимальности Беллмана.

Каково бы не было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так , чтобы доход на данном шаге плюс оптимальный доход на всех последующих шагах был максимальный.

Метод ДП позволяет с успехом решать задачи экономического планирования.

12. Решение задачи о распределении ресурсов методами динамического программирования

Метод динамического программирования позволяет решать многие задачи экономического планирования.

Ситуация: Министерство располагает денежными средствами –– 8 млнусл. ед., которые необходимо распределить между тремя его заводами. Ожидаемый доход предприятия i при условии, что ему выделяют х млнусл. ед., равен fi(x). Исходные данные содержатся в следующей таблице (для простоты полагаем, что денежные суммы выражаются целыми числами от 0 до 8).

Как распределить имеющиеся средства между заводами, чтобы получить наибольшую прибыль?

Пусть в общем случае надо распределить а млнусл. ед. между n заводами. Поступим следующим образом. Будем считать, что сначала все денежные средства мы отдаем первому заводу, потом разделим их между первым и вторым, затем между тремя заводами. Каждый раз вначале распределяем 1 млнусл. ед., затем 2, 3 и т. д.

Обозначим через Fk(x) наибольший доход, который можно получить, разделив сумму х между предприятия 1, 2, …, k, где

Решение задачи будет состоять в последовательном вычислении значений F1(x), F2(x), …, Fn(x) для всех х от 0 до а. Закончим вычислением Fn(a), которое дает оптимальное значение величины дохода.

Прежде всего, найдем F1(x). Поскольку в этом случае все достается только первому предприятию, то F1(x) = f1(x) для любого x.

Предположим, что мы знаем, как лучше разделить х млнусл. ед. между k – 1 предприятиями и какой при этом будет суммарный доход, то есть известны значения Fk – 1(x) для всех х от 0 до а. Теперь распределим эти средства между k предприятиями.

Мы можем выделить заводу k любую сумму от 0 до х. Допустим, что она составляет у млнусл. ед. и прибыль завода в этом случае –– fk(у). Тогда на долю первых k – 1 заводов приходится (х – у) млнусл. ед. Как лучше вложить их мы знаем и известна прибыль Fk – 1(х – у), получаемая в итоге. Отсюда выводим, что суммарный доход k предприятий будет равен Fk – 1(x – у) + fk(у).

Можно было бы выделить заводу k и другую сумму, при этом общий доход мог бы увеличиться. Поэтому надо рассмотреть все возможные варианты вложения средств и выбрать лучший. Следовательно, Обозначим Yk(x) значение y, при котором достигается максимум Fk(x). Таким образом, Yk(x) –– это вложение в предприятие k при условии оптимального распределения х млн усл. ед. между предприятиями 1, 2, …, k. Зная Yn(a) и промежуточные значения Yk(х), можно узнать, какую сумму получит каждое из предприятий при оптимальном распределении денежных средств между ними. Рассмотрим, как это делается для исходных данных в ситуации. Значения Fk(x) и Yk(х), вычисляемые последовательно, будем располагать в таблицах.

Как уже отмечалось, F1(х) = f1(х) для любого х, поэтому сразу получаем доход при финансировании только первого завода. Сведем эти данные в таблицу:

Переходим к распределению денежных средств между двумя заводами.

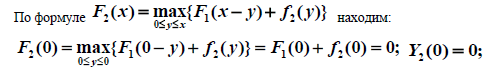
Таким образом, наибольший ожидаемый доход F3(8) = 1,4 млнусл. ед.

Заметим, что на этом последнем шаге максимум достигается в двух случаях: 0,85 + 0,55 = 1,4 и 0,8 + 0,6 = 1,4. Если третьему заводу выделить 3 млнусл. ед., то сколько досталось второму заводу мы узнаем из второй таблицы: Y2(8 – 3) = Y2(5) = 2. Аналогично, первому заводу досталось Y1(5 – 2) = Y1(3) = 3 млнусл. ед. В итоге первому заводу достается 3, второму –– 2, третьему –– тоже 3 млн. усл. ед.

Если же третьему заводу выделить 4 млнусл. ед., то в этом случае Y2(8 – 4) = Y2(4) = 1 и Y1(4 – 1) = Y1(3) = 3. То есть первому заводу достается 3, второму –– 1, третьему –– 4 млнусл. ед.

В каждом из этих случаев общая прибыль составляет 1,4 млнусл. ед.

Заметим, что величина оптимальной прибыли при распределении денежных ресурсов между предприятиями не зависит от их нумерации.