Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Бийский технологический институт (филиал АГТУ им. Ползунова)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Vvedenie_v_matan_differentsialnoe_ischislenie.doc

Скачиваний:

Добавлен:

01.03.2025

Размер:

4.6 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

Свойства непрерывных функций:

Т1. Если функция непрерывна в точке и , то в некоторой - окрестности точки x₀ значения функции имеют тот же знак, что и .

Т2. Если функция непрерывна в точке , то существует - окрестность этой точки, в которой ограничена.

Т3. Если функции непрерывны в точке x₀, то в этой точке непрерывна алгебраическая сумма этих функций, их произведение и (в случае ) частное .

Из всех этих теорем можно получить соответствующие следствия. Например:

Если непрерывна в точке и в любой - окрестности этой точки принимает как положительные, так и отрицательные значения, то .

Согласно пятому определению непрерывности функции в точке, при выполнении равенства функция непрерывна в точке .

Опр. Если в точке x₀ равенство не выполняется (любым образом), то говорят, что точка является точкой разрыва функции , а сама функция в этой точке имеет разрыв.

Классификация точек разрыва функции проводится согласно следующим определениям:

Если , причем все эти числа конечные, то называется точкой устранимого разрыва функции .

имеет разрыв в точке , причем - точка устранимого разрыва. Исправив значения этой функции в точке «0» и положив , мы уже получим непрерывную функцию в точке «0».

Если - конечные числа и , то называется точкой разрыва/скачка.

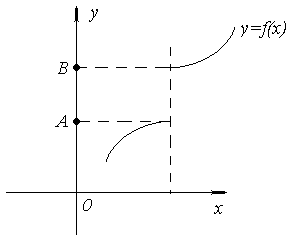
Точки устранимого разрыва и точки разрыва/скачка называются точками разрыва первого рода.

Если в точке хотя бы один из односторонних пределов вовсе не существует или равен , то такая точка разрыва функции называется точкой разрыва второго рода.

, то - функция Дирихле.

Эта функция не имеет точек непрерывности, все точки являются точками разрыва, причем точками разрыва второго рода.

Лекция № 26.

Тема: «Задачи, приводящие к понятию производной. Определение производной. Механический и геометрический смысл производной. Уравнения касательной и нормали к графику функции. Дифференцируемость функции в точке».

Пусть дана функция с областью определения . Предполагается, что вместе с некоторой своей окрестностью.

Точке придадим малое приращение так, чтобы точка тоже принадлежала . Ясно, что равна малому числу. Если предположить, что , то .

называется приращением аргумента рассматриваемой функции в точке . Величина называется приращением функции в точке , соответствующим приращению аргумента .

Опр. Если существует предел отношения приращения функции в точке к соответствующему приращению аргумента при стремлении этого приращения к нулю, то этот предел называется производной функции в точке .

Эта производная обозначается так:

Таким образом: (1)

Рассмотрим механический смысл производной функции.

Пусть материальная точка движется равномерно прямолинейно вдоль оси OS. Отсчет пути ведется от точки О. Зависимость пройденного пути от времени пусть задается формулой: S=s(t). Функция S=s(t) называется законом движения.

Пусть к моменту времени t движущаяся точка прошла путь S(t). Дадим t приращение . К этому моменту времени точка пройдет путь . От момента времени t до следующего момента времени точка пройдет путь: .

Отношение представляет собой среднюю скорость движения точки за промежуток времени от t до . Предел этой скорости движения при называется мгновенной скоростью движения в момент времени t. Таким образом, эта мгновенная скорость равна:

Согласно определению производной функции по формуле (1) имеем:

Это равенство выражает механический смысл производной функции: производная функции с механической точки зрения представляет собой скорость изменения этой функции. В частности, если функция задает закон движения, то производная этой функции представляет собой скорость движения.

Рассмотрим геометрический смысл производной функции.

Пусть функция имеет график, который представляет собой гладко изменяющуюся кривую.

Пусть точке соответствует точка этого графика, а точке соответствует точка графика. Проведем секущую, проходящую через точки и . Обозначим через угол наклона этой секущей к положительному направлению оси OX. Рассматривая прямоугольный имеем: (2)

Дадим определение касательной к графику функции в рассматриваемой точке .

Опр. Касательной к графику функции в точке с абсциссой называется предельное положение секущей , когда . Стремлению вдоль графика функции соответствует стремление .

Если угол наклона этой касательной есть , то имеем:

Из аналитической геометрии известно, что представляет собой угловой коэффициент прямой , т.е. касательной. В этом заключается геометрический смысл производной функции: производная функции в точке задает угловой коэффициент касательной к графику этой функции в точке с абсциссой .

Из (3) следует: (4)

Здесь - это угол наклона касательной к графику функции к оси OX в точке с абсциссой . Используя геометрический смысл производной можно решать соответствующие задачи геометрического характера. Напишем уравнение пучка прямых, проходящих через точку : .

Если точка является точкой графика функции , то, подставляя в уравнение пучка прямых вместо , а вместо , мы получим уравнение касательной к графику этой функции в точке :

Через точку касания проведем прямую, перпендикулярную к касательной. Эта прямая называется нормалью к графику функции в точке этого графика с абсциссой . Угловые коэффициенты взаимно-перпендикулярных прямых обратны по величине и противоположны по знаку, т.е., если k - угловой коэффициент касательной, а - угловой коэффициент нормали, то , поэтому подставляя в выше написанное уравнение пучка прямых вместо , получаем уравнение нормали к графику функции:

Опр. Функция называется дифференцируемой функцией в точке , если она в этой точке имеет производную .

Связь между дифференцируемостью функции и ее непрерывностью выражается теоремой.

Т. Если функция дифференцируема в точке , то она непрерывна в этой точке, обратное утверждение, вообще говоря, неверно.

(Без док-ва)

Опр. Функция называется дифференцируемой на том или ином множестве, если она дифференцируема в каждой точке этого множества.

Замечание: Если существует , то он называется правой производной функции в точке x, а если существует , то он называется левой производной функции.

Лекция № 27.

Тема: «Основные правила дифференцирования. Производная сложной функции. Производные основных элементарных функций».

Существует 6 общих правил для формального вычисления производных функций. Эти правила относятся к любым дифференцируемым функциям, независимо от их конкретного вида.

Постоянный множитель можно выносить из-под знака производной. Это означает следующее: если функция дифференцируема в точке x, а λ – постоянное число, то функция тоже дифференцируема в точке x, причем:
Если функции и дифференцируемы в точке x, то в этой точке дифференцируема алгебраическая сумма этих функций, причем: .

Замечание: Это правило остается верным для случая алгебраической суммы любого конечного числа дифференцируемых функций.

Если функции и дифференцируемы в точке x, то в этой точке дифференцируема функция , причем: .

Замечание: Эта формула обобщается на случай произведения трех, четырех,…, любого конечного числа дифференцируемых функций.

Если функции и дифференцируемы в точке x и , то в этой точке дифференцируема функция , причем: .
(Правило дифференцирования обратной функции): Если функция дифференцируема в точке x и , то обратная функция (если она существует) дифференцируема в соответствующей точке y, причем , где после применения этой формулы вместо нужно подставить : (1)

Схему применения этого правила рассмотрим на примере вычисления производной функции .

- это функция, обратная для функции .

Применяя формулу (1), получаем:

Итак, мы получаем .

По этой же схеме вычисляются производные функций если известны производные соответствующих обратных функций: .

(Правило дифференцирования сложной функции): Если функция дифференцируема в точке , а функция дифференцируема в соответствующей точке , то сложная функция дифференцируема в точке , причем при этом .