42. Метод разложения. Примеры

Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.

Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.

Всякую правильную рациональную дробь , знаменатель которой разложен на множители

можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

где  — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.

Пример .

Представим подынтегральную функцию в виде суммы двух дробей и, используя свойство 50, запишем интеграл в виде суммы двух интегралов. Для каждого из полученных интегралов применим метод внесения под знак дифференциала.

43. Метод подстановки. Примеры

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл . Сделаем подстановку , где  — функция, имеющая непрерывную производную.

Тогда и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

Примеры .

1. Воспользуемся методом замены переменной. Введем новую переменную t по формуле . Тогда  или . Тогда

44. Определенный интеграл. Определение, физическая и геометрическая

Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x0 < x1 < x2 < xn = b Тогда говорят, что произведено разбиение RR отрезка [a;b] Далее выберем произв. точку , i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм ΘR при , если он существует независимо от разбиения R и выбора точек ξi, т.е. (1) Если существует (1), то функция f(x) называется интегрируемой на [a;b] – определение интеграла по Риману.

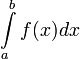
a – нижний предел.

b – верхний предел.

f(x) – подынтегральная функция.

λR - длина частичного отрезка.

σR – интегральная сумма от функции f(x) на [a;b] соответствующей разбиению R.

λR - максимальная длина част. отрезка.

Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Фигура, ограниченная сверху графиком функции у = ƒ(х), снизу — осью Ох, сбоку — прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.

Для этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х0<x1<...<xn) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).

Умножим значением функции ƒ(ci) на  длину ∆xi=xi-xi-1 соответствующего частичного отрезка. Произведение ƒ(ci) • ∆xi равно площади прямоугольника с основанием ∆xi и высотой ƒ(ci). Сумма всех таких произведений

равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:

С уменьшением всех величин Δхi точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что λ = max∆xi →0:

Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

В этом состоит геометрический смысл определенного интеграла.

Пусть материальная точка М перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х — абсцисса движущейся точки М.

Найдем работу А силы F по перемещению точки М вдоль оси Ох из точки х = а в точку х = b (а < b). Для этого отрезок [а; b] точками а = х0, х1, ..., b = хn (х0 < x1 < ... < хn) разобьем на n частичных отрезков [х0; x1], [x1; x2],..., [xn-1; xn]. Сила, действующая на отрезке [xi-1; xi], меняется от точки к точке. Но если длина отрезка Δхi = хi-xi-1 достаточно мала, то сила F на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = ci Î [xi-1; xi]. Поэтому работа, совершенная этой силой на отрезке [xi-1;xi], равна произведению F(ci)•Δхi (Как работа постоянной силы F(ci) на участке [xi-1; xi].) Приближенное значение работы А силы F на всем отрезке [а; b] есть

Это приближенное равенство тем точнее, чем меньше длина Δхi Поэтому за точное значение работы А принимается предел суммы (36.1) при условии, что наибольшая длина λ частичных отрезков стремится к нулю:

В этом состоит физический смысл определенного интеграла.