47.Вариационный ряд.

Множество всех вариант выборки, расположенных в порядке возрастания их значений, вместе с их соответствующими частотами или относительными частотами называется вариационным рядом:

	…
	…
	…

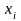
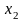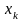
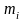
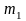
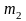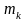
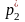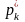
Таблица интервалов, содержащая данную выборку значений случайной величины Х и соответствующие частоты или относительные частоты, называется статистическим рядом. Статистический ряд распределения вероятностей определяется по

исходной выборке объемом n, если анализируемая случайная величина Х является дискретной с известным множеством значений {x₁..x_m }:

Гистограмма – статистический аналог графика плотности вероятности f *(x) случайной величины, и она строится по интервальному статистическомуряду. Гистограмма представляет собой совокупность прямоугольников, построенных, как на основаниях, на интервалах hj статистического ряда с высотой равной статистической плотности вероятности в соответствующем

48.Эпмирическая функция.

Если x₁, x₂, …x_n – выборка значений случайной величины Х, то эмпирической функцией распределения называется функция действительного аргумента x  (- ∞; ∞), обозначаемая через , равная относительной частоте выборочных значений, меньших числа x .

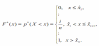
Так как относительная частота значений случайной величины Х, удовлетворяющих неравенству Х < x, в выборке объема n стремится к вероятности выполнения этого неравенства, то при n → ∞ имеем, что 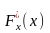= 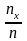→ P(X < x) = F_х(x).

Эмпирическая функция распределения обладает всеми свойствами теоретической функции распределения.

1. Эмпирическая функция распределения является неубывающей функцией, то есть

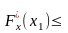
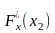при x₁ < x₂ .

2. Справедливы следующие равенства:

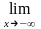
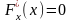и .

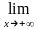
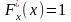3. Все значения эмпирической функции распределения находятся между 0 и 1, то есть

49 Выборочное среднее

Пусть   — выборка из распределения вероятности, определённая на некотором вероятностном пространстве  . Тогда её выборочным средним называется случайная величина

.

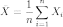Выборочная дисперсия

Пусть 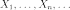  — выборка из распределения вероятности. Тогда

Выборочная дисперсия — это случайная величина

,

где символ 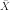  обозначает выборочное среднее.

Несмещённая (исправленная) дисперсия — это случайная величина

.

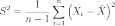50.Распределение 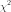  (хи-квадрат) с   степенями свободы — это распределение суммы квадратов   независимых стандартных нормальных случайных величин. Пусть 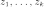  — совместно независимые стандартные нормальные случайные величины, то есть: 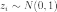 . Тогда случайная величина

имеет распределение хи-квадрат с   степенями свободы, то есть  .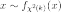

Распределение хи-квадрат является частным случаем гамма-распределения, и имеет вид:

,

где 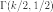  означает Гамма-распределение, а 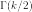  — Гамма-функцию.

Функция распределения имеет следующий вид:

,

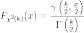где   и   обозначают соответственно полную и неполную гамма-функции.

51 Распределе́ниеСтью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Названо в честь Уильяма СилиГоссета, который первым опубликовал работы, посвящённые распределению, под псевдонимом «Стьюдент». Пусть 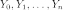  — независимые стандартные нормальные случайные величины, такие что 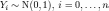 . Тогда распределение случайной величины  , где

называется распределением Стьюдента с   степенями свободы. Пишут 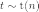 . Её распределение абсолютно непрерывно и имеет плотность

,

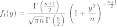где   — гамма-функция Эйлера.

52 Распределе́ниеФи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Пусть 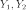  — две независимые случайные величины, имеющие распределение хи-квадрат: 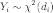 , где 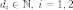 . Тогда распределение случайной величины

,

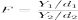
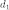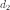называется распределением Фишера (распределением Снедекора) со степенями свободы   и  . Пишут 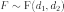 .