42, 43.Закон больших чисел.

Неравенство Чебышева, Лемма Чебышева.

Лемма Чебышева: Пусть среди значений случ. вел-ныZ нет отриц-х, тогда вер-ть того, что в некотором испытании значение этой случ. величины окажется больше, чем А (А-нек. число) оценивается по ф-ле: P(Z>A)M(Z)/A; Равносильно утверждение: P(ZA)1-(M(Z))/A.

Неравенство Чебушева.: Вер-ть того, что в некотором испытании значение величины Yбудет отличаться от математического ожидания этой случайной величины не более чем на  (по абсолютной величине) оценивается по ф-ле:

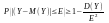
Следствие 1). Пусть Y=(x1+…xn)/n, где х1,х2,…хn-независимы, M(xi)=ai, D(Xi)C, где С- некоторое число i-1,2,…n, тогда справедливо нер-во.

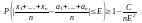
Следствие 2) Пусть имеется n независимых случайных х1,х2,хn чисел, имеющих одинаковые математические ожидания M(Xi)=a и дисперсиями, ограниченными числом С, тогда справедливы неравенства D(Xi)C.

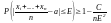
Следствие 3) Пусть имеется n повторных независ. испытаний, в каждом из которых событие может произойти с … n. С каждой вер-тью число успехов nповторн. незав. Испыт. Х=m- биномиальный закон распределения. M(Xбин)=np; D(Xбин)=npq. Рассмотрим нер-во Чебышева: 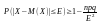, применим получится

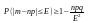Следствие 4) Для частости (доли) признака в повторных независимых испытаниях доля или частостьX=m/n; M(m/n)=p; D(m/n)=pq/n. Применим нер-во Чебышева к этой случайной величине, получим:

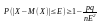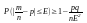; -это также называется нер-вом Бернулли. Следствие 5) Устойчивость среднего арифметического. Практически достоверно можно утверждать, что при достаточно большомn среднее арифметическое случ. величины сколь угодно мало отличается от среднего арифметического их математических ожиданий. Предполагается независимость 

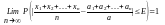Говорят, что среднее число случайных величин сходится к вер-ти их математических ожиданий

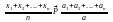
Замечание: Следствие 5 получается из следствия 1, если в правой части перейти к пределу при n

Следствие 6) Устойчивость частости (доли) Практически достоверно, что доля успехов в n повторных независимых испытаниях сколь угодно мало отличается от их вер-ти успеха (при достаточно большом числе испытания n) 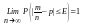,или

же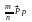 Замечание: следствие 6 получ. Из следствия 4, если в правой части перейти к пределу при n.

44. Центральная предельная теорема

Многие непрерывные случайные величины имеют нормальное распределение. Это обстоятельство во многом определяется тем, что суммирование большого числа случайных величин с самыми разными законами распределения приводит к нормальному распределению этой суммы.

Указанное свойство подтверждается интегральной предельной теоремой, доказанной Ляпуновым.

Теорема. Если случайнаявеличинаХ представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, тоХ имеет распределение, близкое к нормальному.

Центральная предельная теорема имеет огромное значение для практики.

Допустим, определяется некоторый экономический показатель, например, потребление электроэнергии в городе за год. Величина суммарного потребления складывается из потребления энергии отдельными потребителями, которая имеет случайные значения с разными распределениями. Теорема утверждает, что в этом случае, какое бы распределение не имели отдельные составляющие, распределение результирующего потребления будет близко к нормальному.

О днако следует иметь в виду, что при усилении влияния отдельных факторов могут появляться отклонения от нормального распределения результирующего параметра, например, может возникнуть асимметрия или эксцесс. Поэтому большое значение на практике уделяется экспериментальной проверке выдвинутых гипотез, в том числе и гипотезы о нормальном распределении.

Поэтому, в некоторых случаях приходится рассматривать распределение случайной величины, имеющие определенные отличия от нормального. Для оценки этого отличия введены специальные характеристики. К ним относятся, в частности, асимметрия и эксцесс.

Асимметрией распределения случайной величины называется отношение центрального момента третьего порядка к кубу среднего квадратичного отклонения:

.

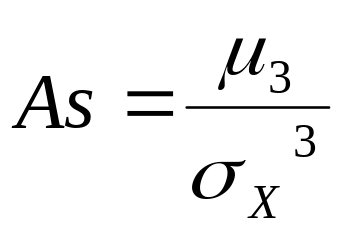Эксцессом распределения случайной величины называют число, определяемое выражением:

.

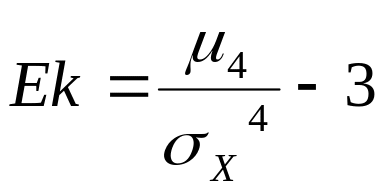Для нормального распределения 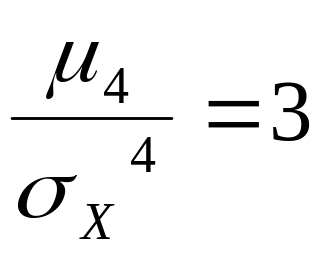, поэтому эксцесс равен нулю.

45Стати́стика — отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических (количественных или качественных) данных; изучение количественной стороны массовых общественных явлений в числовой форме^[1].Статистика разрабатывает специальную методологию исследования и обработки материалов: массовые статистические наблюдения, метод группировок, средних величин, индексов, балансовый метод, метод графических изображений и другие методы анализа статистических данных.

46.Основу статистического исследования составляет множество данных, полученных в результате измерения одного или нескольких признаков. Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений 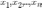 случайной величины  , является выборкой, а гипотетически существующая (домысливаемая) — генеральной совокупностью. Генеральная совокупность может быть конечной (число наблюдений N = const) или бесконечной (N = ∞), а выборка из генеральной совокупности — это всегда результат ограниченного ряда   наблюдений. Число наблюдений  , образующих выборку, называется объемом выборки. Если объем выборки   достаточно велик (n → ∞) выборка считается большой, в противном случае она называется выборкой ограниченного объема. Выборка считается малой, если при измерении одномерной случайной величины   объем выборки не превышает 30 (n <= 30), а при измерении одновременно нескольких (k) признаков в многомерном пространстве отношениеn к k не превышает 10 (n/k < 10). Выборка образует вариационный ряд, если ее члены являются порядковыми статистиками, т. е. выборочные значения случайной величины Х упорядочены по возрастанию (ранжированы), значения же признака называютсявариантами.