39.Ф.Мног.Слювел.
Функцией распределения n-мерной случайной величиной (Х1, Х2, …, Хn)
называется вероятность выполнения n неравенств вида Хi < xi:
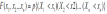
39 Многомерные функции распределения
Пусть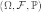 
фиксированное
вероятностное пространство, и 
—
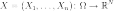случайный вектор. Тогда распределение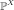 
,
называемоераспределением
случайного вектора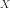 
или совместным
распределением случайных величин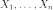 
,
является вероятностной мерой на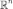 
.
Функция этого распределения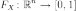 
задаётся
по определению следующим образом:
,
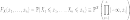где 
в
данном случае обозначает декартово
произведение множеств.
Свойства
многомерных функций распределения
аналогичны одномерному случаю. Также
сохраняется взаимно-однозначное
соответствие между распределениями
на
и
многомерными функциями распределения.
Однако, формулы для вычисления
вероятностей существенно усложняются,
и потому функции распределения редко
используются для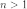 
.
40..Пусть
определено произвольное вероятностное
пространство
,
и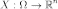 
случайная
величина (или
случайный вектор).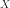 
индуцирует
вероятностную меру
на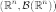 
,
называемую распределением случайной
величины
.
Определение
3. Если
распределение
абсолютно
непрерывно относительно меры Лебега,
то его плотность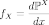 
называется
плотностью случайной величины
.
Сама случайная величина
называется
абсолютно непрерывной.
Таким образом для абсолютно непрерывной случайной величины имеем:
.Свойства плотности вероятности
Плотность вероятности определена почти всюду. Если
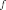является
плотностью вероятности 
и 
почти
всюду относительно меры Лебега, то и
функция 
также
является плотностью вероятности
.
Интеграл от плотности по всему пространству равен единице:
.
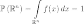Обратно,
если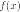 
—
неотрицательная п.в. функция, такая
что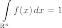 
,
то существует абсолютно непрерывная
вероятностная мера
на
такая,
что
является
её плотностью.
Замена меры в интеграле Лебега:
,
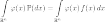где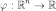 
любая
борелевская функция, интегрируемая
относительно вероятностной меры
.
41, СОБЫТИЯ СЛУЧАЙНЫЕ НЕЗАВИСИМЫЕ
— такие случайные события А и В, для которых вероятность Р одновременного наступления 2-х событий А к В равна произведению вероятностей наступления каждого из них в отдельности: Р(АВ) = Р(А)·Р(В). Аналогично определение независимости п случайных событий. Это определение распространяется на независимость случайных величин, а именно, случайные величины X1, Х2, ..., Хп независимы, если для любой группы Хi1, Xi2, ..., Xik, этих величин верно равенство: Р(Хi1 ≤ хi1, Хi2 ≤ хi2, ..., Хik≤ xik) = Р(Хi1 ≤ хi2)Р(Хi2 ≤хi2)...(Р(Хik ≤ хik); 1≤ k ≤ n. При решении геол. задач методами теории вероятностей и математической статистики корректная оценка зависимости изучаемых величин часто является наиболее сложной и ответственной частью исследования..