
- •30,. Дискретные случайные величины. Законы
- •32.Мат ожидание дсв и их свойства.
- •33,Дисперсия (дискретной ) случайной величины.
- •35. Моменты случайной величины
- •36, Ковариация .
- •37,Коэффициент корреляции и его св-ва.
- •39.Ф.Мног.Слювел.
- •39 Многомерные функции распределения
- •.Свойства плотности вероятности
- •42, 43.Закон больших чисел.
- •44. Центральная предельная теорема
- •47.Вариационный ряд.
- •48.Эпмирическая функция.
- •49 Выборочное среднее
- •Выборочная дисперсия
35. Моменты случайной величины
Моме́нтслуча́йной величины́ — числовая характеристика распределения данной случайной величины. Определения
Если
дана случайная величина Х определённая
на некотором вероятностном пространстве,
то:К-мнача́льным моментом случайной
величины Х где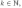 называется величина
называется величина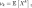 если
математическое ожидание
если
математическое ожидание
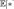 в правой части этого равенства определено;
К-м центра́льным моментом случайной
величины называется величина
в правой части этого равенства определено;
К-м центра́льным моментом случайной
величины называется величина
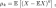 К-м
абсолю́тным и К -м центральным абсолютным
моментами случайной величины называется
соответственно величины
К-м
абсолю́тным и К -м центральным абсолютным
моментами случайной величины называется
соответственно величины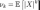 и
и
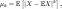 К-м
факториальным моментом случайной
величины Х называется величина
К-м
факториальным моментом случайной
величины Х называется величина
если математическое ожидание в правой части этого равенства определено.
Абсолютные моменты могут быть определены не только для целых k, но и для любых положительных действительных в случае, если соответствующие интегралы сходятся.
36, Ковариация .
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий используют и другие характеристики. К их числу относятся ковариация и коэффициент коррекции.
Опр.
Ковариацией
между случайными величинами Х и Y
называется число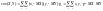 ,
где
,
где .Для
непрерывных случайных величин X
и Y
используют формулу
.Для
непрерывных случайных величин X
и Y
используют формулу
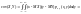
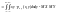 .
Покажем, что если случайные величины
Х и Y
независимы, то
.
Покажем, что если случайные величины
Х и Y
независимы, то
 .
Пусть Х и Y—непрерывные
случайные величины
.
Пусть Х и Y—непрерывные
случайные величины
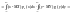
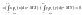
37,Коэффициент корреляции и его св-ва.
Опр. Коэффициентом корреляции случ. величин Х и Уназыв. число, вычисляемое по ф-ле: =(M(XY)-M(X)M(Y))/(XY), где X=D(X), Y=D(Y), а M(XY)-M(X)M(Y)- ковариация KXY. Модуль коэфф-та корреляции не превосходит 1, т.е. -11.; Если модуль коэфф-та ||=1, то между случайными величинами
существует линейная функциональная зависимость.; Пусть - коэфф-нт корреляции случайных величин X и Y: =(M(XY)-M(X)M(Y))/(XY) ; Заменяя в последнем выражении входящие величины на их выборочные оценки, получаем формулу для
вычисления
выборочного коэфф-нта корреляции r:
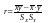
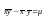 -выборочная
ковариация, т.к.
-выборочная
ковариация, т.к.
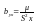 ,
,
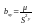 ;
;
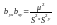 ;
;
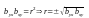 ,
«+»,если
,
«+»,если
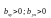 ;
«-» если
;
«-» если
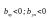 .Если
r>0,то
связь между переменной называется
прямой.
.Если
r>0,то
связь между переменной называется
прямой.
Если r<0- связь называется обратной. Связь между переменными признается тесной, если |r|0,7; умеренной если 0,4|r|0,7; слабой если |r|<0,4. Основное св-во коэфф-та корреляции: |r|1.; Предельное значение коэфф-та корреляции:
|r|=1,т.ит.т.к. byx*bxy=1 => прямые регрессии совпадают.
2) r=0 т.ит.т.к. µ=0 byx=0 и bxy=0 => прямые регрессии перпендикулярны.; Если r=0 то говорят, что между переменными х и у отсутствует линейная корреляционная зависимость.
38.Многомерной случ. вел.
Многомерные случайные величины Совокупность произвольного числа n одномерных случайных величин Хi, i = 1, …, n, которые принимают значение в результате проведения одного и того же опыта, называется n-мерной случайной величиной (Х1, Х2, …, Хn). Ее можно интерпретировать как случайную точку или случайный вектор в n-мерном пространстве.
