30,. Дискретные случайные величины. Законы

распределения биномиальное, геометрическое и Пуассона.

Опр. Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ω_х—конечно или счетно.

Опр.Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (х_i, р_i), где x_i—возможные значения случайной величины, а p_i—вероятности, с которыми случайная величина принимает эти значения, т.е. 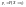, причем 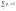.Опр. Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения с вероятностями 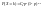. 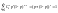Опр. Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения с вероятностями . Обозначают , т.е. случайная величина Х имеет распределение Пуассона с параметром λ. 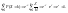Опр. Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения 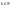с вероятностями 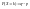, где q=1-p.

.

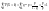31.Функция распределения и плотность вероятности непрерывной случайной величины

Если функция распределения Fx (x) непрерывна, то случайная величина x называется непрерывной случайной величиной.

Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины px (x), которая связана с функцией распределения Fx (x) формулам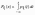и

и .

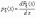
Отсюда, в частности, следует, что для любой случайной величины .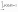

32.Мат ожидание дсв и их свойства.

Опр. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Обозначают математическое ожидание случайной величины Х через MX или М(Х). 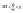– случайная величина Х принимает конечное число значений. 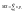– принимает счетное число значений, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Свойства математического ожидания:

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: M(C)=C. Будем рассматривать постоянную С как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью 1. Следовательно, .

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X).

Ряд распределения случайной величины СХ

Математическое ожидание случайной величины СХ .

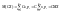Опр. Случайные величины X₁,X₂,…,X_n называются независимыми, если для любых числовых множеств B₁,B₂,…,B_n .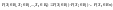

33,Дисперсия (дискретной ) случайной величины.

Опр.: Пусть закон распределения случ. величины Х имеет вид:

Х:

Дисперсией D(X)- этой случ. величины называется число, вычисл. по ф-ле:

хх этой случ. величины около её мат. ожидания.

Св-ва дисперсии: 1)D(С)=0, С- пост. случ. величина.

2)D(X)=в квадратеD(X).

3)Пусть случ. величины X иY-независимы =>D(XY)=D(X)+D(Y). 4)D(X)=M(X в квадрате) – М в квадрате(Х).

5)Пусть случ. величины Х1,Х2,…Хn- независимы и D(X1)=…=D(Xn)= в квадрате. ; тогда D((x1+…+xn)/n)=( в квадрате)/n). Замечание: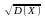 – назыв. среднеквадратическим отклонением случ. величины X и часто обозначается через(сигма).

Теорема: Пусть случ. величина Х биномиально распределена с параметрами n и p, тогда M(X)=np; D(X)=npq; q=1-p; M(X/n)=p; D(X/n)=(pq)/n.

Док-во: Пусть Х- число наступившего события А в nповторн. независ. исп-ях в каждом из которых соб А наступает с вер-тью р => Х=Х1+Х2+…+Хn,где Xi- число наступ-его соб-я А в i испытаний (1in). Х1,Х2,…Хn– независ. и одинаково распределены. 1i n.

M(Xi)=0q+1p=p. ; 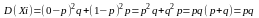M(X)=M(X1+…+Xn)=M(X1)+…+M(Xn)=p+…+p=np.

D(X)=D(X1+…+Xn)=D(X1)+…+D(Xn)=pq+..+pq=npq. Теорема доказана.

Пример: Пусть Х-бином. Распред-а n=3, p=0,8 ;M(X)=30,8=2,4 ; D(X)=30,80,2==0,48.

34.Основные числовые характеристики дискретных и непрерывных случайных величин: математическое ожидание, дисперсия и среднее квадратическое отклонение. Их свойства и примеры.

Математическим ожиданием дискретной случайной величины называ-ется сумма произведений ее возможных значений на соответствующие им вероятности:        М(Х) = х₁р₁ + х₂р₂ + … + х_пр_п .     

Дисперсией (рассеянием) случайной величины называется математи-ческое ожидание квадрата ее отклонения от ее математического ожидания:   D(X) = M (X – M(X))².                                                (7.6)