Найбільш поширеним методом математичного визначення місцерозташування складських центрів є метод центру тяжіння, що полягає в мінімізації відстані до існуючих об’єктів (рис.4.4.1).

4

3

2 ,5

2

1

0

0 1 2 3 4 4,5 5 6 7 8 9

Рис.4.4.1 Визначення методом центру тяжіння місця розташування розподільчого центру, що обслуговує 4 (чотири) торговельні точки

Суть методу полягає в наступному. На карту місцевості, де ми збираємось визначити оптимальне місце для розміщення розподільчого центру, накладаємо сітку системи координат. А далі математичними розрахунками знаходимо координати місця, де відповідно до критеріїю – „мінімальності відстаней” можна „ставити” РЦ:

Xм1 + Xм2 + Xм3 + Xм4 2 + 2 + 6 + 8 18

Xрц = -------------------------------------------- = --------------------------- = ----------- = 4,5

4 4 4

Yм1 + Yм2 + Yм3 + Yм4 3 + 2 + 3 + 2 10

Yрц = ------------------------------------------ = ------------------------------ = ----------- = 2,5

4 4 4

5.2 Розрахунок використання наявного рухомого складу

Умова задачі З двох складів вивозять однотипний вантаж на тягачах з причепами. Відомо, що для вивезення вантажу з першого терміналу один тягач має мати два причепи, а другий – чотири причепи. Кількість вантажу, яка перевозиться одним тягачем з першого терміналу, становить 12 т, а з другого – 20 т. АТП має 8 тягачів і 24 причепи. Необхідно розподілити тягачі і причепи таким чином, щоб забезпечити їх максимальну продуктивність.

Розв’язання

Умову задачі можна записати рівняннями:

- рівняння для тягачів

- рівняння для причепів

де - кількість тягачів на терміналі 1;

- кількість тягачів на терміналі 2.

З умови задачі записуємо рівняння продуктивності:

Дослідимо перші два рівняння на максимум і визначимо значення і .

З першого рівняння ці значення становитимуть (тягачі), а з другого - (причепи).

Побудуємо графік у відповідності з результатами і (рис. 6.2.1).

Рис. 6.2.1 Графік визначення оптимального завантаження автомобілів і тягачів

На рис. 6.2.1 зображена точка перетину двох прямих з координатами . Отже, на перший термінал слід відправити 4 тягачі, і на другий – 4 тягачі.

Оскільки один тягач на першому терміналі потребує 2 причепи, а на другому – 4, то причепи слід розподілити таким чином:

• на перший термінал: ;

• на другий термінал: .

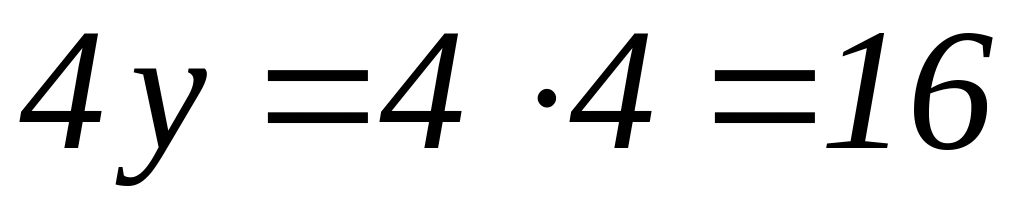Максимальна продуктивність становитиме:

тон.

Завдання для аудиторії: До наступного заняття при допомозі Excel-таблиці створити модель розв’язання вище зазначеної задачі